Ellipsin kaarevuusympyrät
Minkä tahansa käyrän kaartumista jossakin sen pisteessä voidaan mitata
muodostamalla pisteen kautta kulkeva ympyräviiva, jonka kaartuminen on yhtä
voimakasta kuin käyrän kaartuminen kyseisessä pisteessä. Ympyrää kutsutaan
käyrän kaarevuusympyräksi ja ympyrän sädettä käyrän kaarevuussäteeksi
kyseisessä pisteessä. Kaarevuus on kaarevuussäteen käänteisarvo. Kaarevuus on
siis sitä suurempi, mitä jyrkemmin käyrä kaartuu.
Edellä sanottu ei luonnollisestikaan ole kaarevuusympyrän määrittely: ’yhtä
voimakas kaartuminen’ vaatii täsmällisen määrittelyn. Tämä voidaan tehdä
differentiaalilaskennan keinoin, mutta tässä yhteydessä siihen ei lähemmin
paneuduta.
Usein käyrän kulku voidaan hahmotella, jos sen kaarevuusympyrät riittävän
monissa pisteissä tunnetaan. Ellipsin tapauksessa riittää melko hyvin tuntea
akseleiden päätepisteisiin liittyvät ympyrät. Nämä saadaan yksinkertaisella
geometrisella konstruktiolla:
Applet created on 3.1.2005 by SKK with
CabriJava
Piirretään ellipsiä ympäröivä suorakulmio 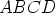 , jonka sivut ovat ellipsin
pääakseleiden suuntaiset ja pituudeltaan siis
, jonka sivut ovat ellipsin
pääakseleiden suuntaiset ja pituudeltaan siis  ja
ja  . Suorakulmiolle
piirretään jompikumpi lävistäjä, esimerkiksi
. Suorakulmiolle
piirretään jompikumpi lävistäjä, esimerkiksi 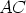 ja tälle normaalit kahden muun
kärkipisteen, tällöin
ja tälle normaalit kahden muun
kärkipisteen, tällöin  ja
ja  , kautta. Pisteen
, kautta. Pisteen  kautta kulkeva normaali
leikkaa ellipsin ison akselin pisteessä
kautta kulkeva normaali
leikkaa ellipsin ison akselin pisteessä  ja pikku akselin jatkeen pisteessä
ja pikku akselin jatkeen pisteessä  .
Nämä ovat ison akselin toiseen päätepisteeseen ja pikku akselin toiseen
päätepisteeseen liittyvien kaarevuusympyröiden keskipisteet. Kaarevuusympyrät
voidaan siis piirtää.
.
Nämä ovat ison akselin toiseen päätepisteeseen ja pikku akselin toiseen
päätepisteeseen liittyvien kaarevuusympyröiden keskipisteet. Kaarevuusympyrät
voidaan siis piirtää.
Vastakkaisiin päätepisteisiin liittyvät symmetriset kaarevuusympyrät saadaan
vastaavasti pisteen  kautta kulkevan normaalin avulla.
kautta kulkevan normaalin avulla.
Jos ellipsin akselit tunnetaan, voidaan kaarevuusympyrät konstruoida. Itse
ellipsin voi tällöin likimääräisesti hahmotella vapaalla kädellä, kuten kuvion
oikean ylänurkan osasta ilmenee: Punainen ellipsinkaari liittyy kummankin
akselin päätepisteen lähellä piirustustarkkuuden rajoissa varsin tarkoin
vastaavaan kaarevuusympyrään ja siirtyy ympyrältä toiselle melko lyhyellä
matkalla.
Oheinen kuvio on laadittu Cabri-Geometria-ohjelmalla. Cabri-dokumentissa
ellipsin kokoa ja muotoa voidaan muuttaa tarttumalla hiirellä  -keskisiin
ympyröihin ja kasvattamalla tai pienentämällä näiden säteitä. Muu konstruktio
muuttuu tällöin vastaavasti.
-keskisiin
ympyröihin ja kasvattamalla tai pienentämällä näiden säteitä. Muu konstruktio
muuttuu tällöin vastaavasti.
Harjoitustehtäviä
Piirrä ellipsejä kuvatulla menetelmällä ja arvioi tulosten hyvyyttä. Miten
piirtämiseen tarkuuteen vaikuttaa ellipsin akselien suhde? Osoita esitetyn
konstruktion perusteella, että kaarevuusympyröiden säteet ovat  ja
ja  .
Perehdy kaarevuussäteiden laskemiseen differentiaalilaskennan avulla ja osoita,
että tällä tavoin saadaan em. arvot kaarevuussäteille, ts. että esitetty konstruktio
todellakin antaa kaarevuusympyrät.
.
Perehdy kaarevuussäteiden laskemiseen differentiaalilaskennan avulla ja osoita,
että tällä tavoin saadaan em. arvot kaarevuussäteille, ts. että esitetty konstruktio
todellakin antaa kaarevuusympyrät.
Linkkejä
Vastaava Cabri-dokumentti
Cabri-ohjeet
Simo K. Kivelä 07.04.2004
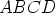 , jonka sivut ovat ellipsin
pääakseleiden suuntaiset ja pituudeltaan siis
, jonka sivut ovat ellipsin
pääakseleiden suuntaiset ja pituudeltaan siis  ja
ja  . Suorakulmiolle
piirretään jompikumpi lävistäjä, esimerkiksi
. Suorakulmiolle
piirretään jompikumpi lävistäjä, esimerkiksi 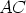 ja tälle normaalit kahden muun
kärkipisteen, tällöin
ja tälle normaalit kahden muun
kärkipisteen, tällöin  ja
ja  , kautta. Pisteen
, kautta. Pisteen  kautta kulkeva normaali
leikkaa ellipsin ison akselin pisteessä
kautta kulkeva normaali
leikkaa ellipsin ison akselin pisteessä  ja pikku akselin jatkeen pisteessä
ja pikku akselin jatkeen pisteessä  .
Nämä ovat ison akselin toiseen päätepisteeseen ja pikku akselin toiseen
päätepisteeseen liittyvien kaarevuusympyröiden keskipisteet. Kaarevuusympyrät
voidaan siis piirtää.
.
Nämä ovat ison akselin toiseen päätepisteeseen ja pikku akselin toiseen
päätepisteeseen liittyvien kaarevuusympyröiden keskipisteet. Kaarevuusympyrät
voidaan siis piirtää.
 kautta kulkevan normaalin avulla.
kautta kulkevan normaalin avulla.
 -keskisiin
ympyröihin ja kasvattamalla tai pienentämällä näiden säteitä. Muu konstruktio
muuttuu tällöin vastaavasti.
-keskisiin
ympyröihin ja kasvattamalla tai pienentämällä näiden säteitä. Muu konstruktio
muuttuu tällöin vastaavasti.
 ja
ja  .
Perehdy kaarevuussäteiden laskemiseen differentiaalilaskennan avulla ja osoita,
että tällä tavoin saadaan em. arvot kaarevuussäteille, ts. että esitetty konstruktio
todellakin antaa kaarevuusympyrät.
.
Perehdy kaarevuussäteiden laskemiseen differentiaalilaskennan avulla ja osoita,
että tällä tavoin saadaan em. arvot kaarevuussäteille, ts. että esitetty konstruktio
todellakin antaa kaarevuusympyrät.