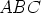 mielivaltainen kolmio. Tämän sivuille asetetaan tasasivuiset
kolmiot
mielivaltainen kolmio. Tämän sivuille asetetaan tasasivuiset
kolmiot 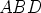 ,
, 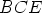 ja
ja 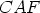 siten, että kärjet
siten, että kärjet 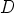 ,
, 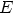 ja
ja 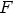 osoittavat
alkuperäisestä kolmiosta poispäin. Tasasivuisten kolmioiden keskipisteet olkoot
osoittavat
alkuperäisestä kolmiosta poispäin. Tasasivuisten kolmioiden keskipisteet olkoot
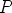 ,
, 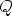 ja
ja 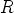 .
.
Ranskan keisari Napoleonin lähipiiriin kuului useita merkittäviä matemaatikkoja kuten Gaspard Monge, Pierre Simon de Laplace ja Jean Baptiste Joseph Fourier.
Monge oli maineikkaan erityiskorkeakoulun École Polytechniquen professori, joka loi deskriptiivisen geometrian alaan kuuluvan, aikoinaan sotasalaisuutenakin pidetyn sotilaallisen ja teknillisen suunnittelun apuvälineen, Mongen projektion.
Laplace oli École Militairen professori, tunnettu taivaanmekaniikkaa, matemaattista fysiikkaa ja todennäköisyyslaskentaa koskevista tutkimuksistaan. Hänen mukaansa on matemaattisen fysiikan ehkä merkittävin differentiaaliyhtälö saanut nimensä, samoin monien soveltajien käyttämä integraalimuunnos.
Myös Fourier oli École Polytechniquen professori; teoksessaan Théorie analytique de la chaleur (= lämpö) hän esitti myöhemmin Fourier-analyysina tunnetun menetelmän.
Jokainen näistä matemaatikoista osallistui myös tavalla tai toisella Napoleonin ajan sotiin tai hallintoon. Keisari itse puolestaan harrasti matematiikkaa.
Muun ohella Napoleonin nimi onkin jäänyt historiaan eräässä alkeisgeometrian lauseessa, joka perustuu alla olevaan kuvioon:
Olkoon 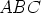 mielivaltainen kolmio. Tämän sivuille asetetaan tasasivuiset
kolmiot
mielivaltainen kolmio. Tämän sivuille asetetaan tasasivuiset
kolmiot 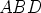 ,
, 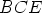 ja
ja 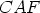 siten, että kärjet
siten, että kärjet 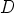 ,
, 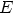 ja
ja 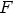 osoittavat
alkuperäisestä kolmiosta poispäin. Tasasivuisten kolmioiden keskipisteet olkoot
osoittavat
alkuperäisestä kolmiosta poispäin. Tasasivuisten kolmioiden keskipisteet olkoot
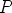 ,
, 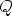 ja
ja 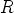 .
.
Applet created on 29.12.2004 by SKK with CabriJava
Tehtävä 1: Mikä on lauseen väite?
Vihjeeksi seuraavaa: Napoleonin lause koskee kolmiota 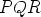 . Huomiota
kannattaa kiinnittää kolmion sivujen pituuksiin ja kolmion keskipisteeseen.
. Huomiota
kannattaa kiinnittää kolmion sivujen pituuksiin ja kolmion keskipisteeseen.
Tarkasteluja helpottaa, jos piirtää useita erilaisia kolmioita 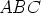 ja konstruoi
vastaavan kolmion
ja konstruoi
vastaavan kolmion 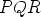 . Apuna voi myös käyttää dynaamisen geometrian
ohjelmia, esimerkisi Cabri-Geometriaa (jolla yllä oleva kuva on tehty). Tällöin
konstruktio tehdään vain kerran ja sen jälkeen siirrellään lähtökohtina olevia
pisteitä
. Apuna voi myös käyttää dynaamisen geometrian
ohjelmia, esimerkisi Cabri-Geometriaa (jolla yllä oleva kuva on tehty). Tällöin
konstruktio tehdään vain kerran ja sen jälkeen siirrellään lähtökohtina olevia
pisteitä 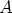 ,
, 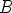 ja
ja 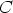 , jolloin konstruktioperiaate säilyy ja kuvio muuntuu
vastaavasti.
, jolloin konstruktioperiaate säilyy ja kuvio muuntuu
vastaavasti.
Tehtävä 2: Miten Napoleonin lauseen voisi todistaa?
Äkkiä ajatellen lähestymistapoja voisi olla ainakin kolme: puhdas geometrinen, ehkä sopivaan apupiirrokseen perustuva; vektorialgebra; perinteinen analyyttinen geometria (koordinaattigeometria). Hieman vieraampi, mutta usein varsin näppärä on kompleksilukualgebra.
Tehtävä 3: Voisiko lauseen yleistää nelikulmioille? Entä 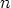 -kulmioille?
Miten?
-kulmioille?
Miten?
Vihjeeksi tieto, että voi, mutta ei rajoituksetta. Millainen on rajoitus? Tätäkin voi tutkia dynaamisen geometrian ohjelmistoilla.
Linkkejä
Vastaava Cabri-dokumentti
Napoleonin lause todistuksineen
Cabri-ohjeet
Simo K. Kivelä 03.01.2005