 sivuille (kolmion
sivuille (kolmion 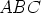 ulkopuolelle) asetetaan
tasasivuiset kolmiot
ulkopuolelle) asetetaan
tasasivuiset kolmiot 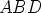 ,
, 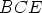 ja
ja 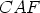 ; näiden keskipisteet olkoot
; näiden keskipisteet olkoot 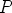 ,
, 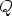 ja
ja 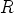 . Tällöin kolmio
. Tällöin kolmio 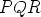 on tasasivuinen ja sen keskipiste yhtyy alkuperäisen
kolmion keskipisteeseen (so. keskijanojen leikkauspisteeseen).
on tasasivuinen ja sen keskipiste yhtyy alkuperäisen
kolmion keskipisteeseen (so. keskijanojen leikkauspisteeseen).
Napoleonin lause on seuraava:
Mielivaltaisen kolmion  sivuille (kolmion
sivuille (kolmion 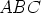 ulkopuolelle) asetetaan
tasasivuiset kolmiot
ulkopuolelle) asetetaan
tasasivuiset kolmiot 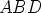 ,
, 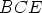 ja
ja 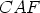 ; näiden keskipisteet olkoot
; näiden keskipisteet olkoot 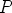 ,
, 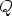 ja
ja 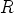 . Tällöin kolmio
. Tällöin kolmio 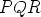 on tasasivuinen ja sen keskipiste yhtyy alkuperäisen
kolmion keskipisteeseen (so. keskijanojen leikkauspisteeseen).
on tasasivuinen ja sen keskipiste yhtyy alkuperäisen
kolmion keskipisteeseen (so. keskijanojen leikkauspisteeseen).
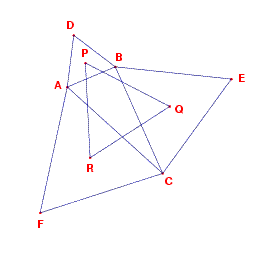
Geometrisia lauseita todistetaan usein piirtämällä sopivia apupiirroksia ja päättelemällä kuvion pisteistä, suorista, janoista, ympyröistä jne. erilaisia asioita. Ajatustapa on peräisin antiikin kreikkalaisilta ja elänyt ns. euklidisen geometrian opetuksessa vuosisatoja ellei -tuhansia.
Paljon myöhemmin syntynyttä algebraa voidaan kuitenkin myös käyttää. Tämä voi tapahtua analyyttisen geometrian (koordinaattigeometrian) muodossa tarkastelemalla pisteitä koordinaattien avulla sekä suoria ja ympyröitä niiden yhtälöiden avulla. Analyyttisen geometrian loi ranskalainen filosofi ja matemaatikko René Descartes 1600-luvulla. (Descartes kuoli vuonna 1650 Tukholmassa, jonne Ruotsin kuningatar Kristiina oli kutsunut hänet filosofian opettajakseen. Kylmä talvi, koleat huoneet, aamulla kello viisi alkaneet oppitunnit kuningattarelle mursivat hänen terveytensä.)
Toinen vaihtoehto on vektorialgebran käyttö. Tämä on viime 1800-luvulla syntynyttä, luojina lähinnä irlantilainen William Rowan Hamilton ja saksalainen Hermann Grassmann.
Kolmas mahdollisuus on kompleksilukualgebra, jonka esitti johdonmukaisessa muodossa erittäin monipuolinen saksalainen matemaatikko Carl Friedrich Gauss 1800-luvun alussa. (Tosin norjalainen Caspar Wessel oli esittänyt kompleksitason käsitteen jo ennen Gaussia, mutta hänen tanskankielistä työtään ei tunnettu.)
Kompleksilukualgebra antaa ehkä vahvimman työkalun Napoleonin lauseen todistamiseen. Syynä on ennen muuta se, että tarvittavat 60 asteen kierrot on helposti hallitavissa kompleksilukujen avulla.
Kiertotekijä. Muotoa 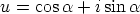 olevaa kompleksilukua voidaan kutsua
kiertotekijäksi, koska sillä kertominen kiertää kompleksilukua kulman
olevaa kompleksilukua voidaan kutsua
kiertotekijäksi, koska sillä kertominen kiertää kompleksilukua kulman 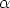 verran
origon ympäri. Tämän voi tarkistaa tämän kirjoittamalla mielivaltaisen
kompleksiluvun
verran
origon ympäri. Tämän voi tarkistaa tämän kirjoittamalla mielivaltaisen
kompleksiluvun 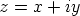 napakoordinaattimuotoon
napakoordinaattimuotoon 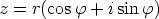 ja laskemalla tulon
ja laskemalla tulon 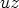 . Tulos saadaan käyttämällä sinin ja kosinin
yhteenlaskukaavoja.
. Tulos saadaan käyttämällä sinin ja kosinin
yhteenlaskukaavoja.
Tarkoittakoon 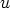 seuraavassa 60 asteen suuruista kiertoa:
seuraavassa 60 asteen suuruista kiertoa:
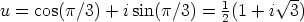 . Koska kolme 60 asteen kiertoa merkitsee
yhteensä 180 asteen kiertoa, on
. Koska kolme 60 asteen kiertoa merkitsee
yhteensä 180 asteen kiertoa, on 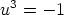 eli
eli 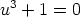 . Tämä voidaan jakaa
tekijöihin:
. Tämä voidaan jakaa
tekijöihin: 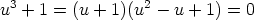 . Koska
. Koska 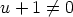 , on kyseisellä
kiertotekijällä ilmeisestikin ominaisuus
, on kyseisellä
kiertotekijällä ilmeisestikin ominaisuus 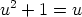 .
.
Tämän yhtälön voi luonnollisestikin tarkistaa myös sijoittamalla siihen
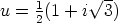 . Se voidaan lisäksi tulkita vektoreiden yhteenlaskuksi:
jos piirretään origosta alkavat pisteisiin
. Se voidaan lisäksi tulkita vektoreiden yhteenlaskuksi:
jos piirretään origosta alkavat pisteisiin 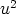 ja
ja 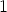 päättyvät vektorit ja
lasketaan ne yhteen, saadaan
päättyvät vektorit ja
lasketaan ne yhteen, saadaan 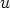 . Kompleksilukujen yhteenlaskuhan on
vektoriyhteenlaskua.
. Kompleksilukujen yhteenlaskuhan on
vektoriyhteenlaskua.
Lauseen todistus. Kolmion kärkipisteitä esittävät kompleksiluvut olkoot  ,
,
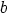 ja
ja  . Siis
. Siis 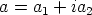 , kun pisteen
, kun pisteen 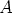 koordinaatit ovat
koordinaatit ovat 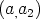 ,
jne. Esitystä reaali- ja imaginaariosan avulla ei seuraavassa kuitenkaan
tarvita.
,
jne. Esitystä reaali- ja imaginaariosan avulla ei seuraavassa kuitenkaan
tarvita.
Tasasivuisen kolmion 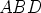 kärki
kärki 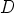 kompleksilukuna on
kompleksilukuna on 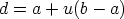 .
Kyseessä on vektorisumma: origosta pisteeseen
.
Kyseessä on vektorisumma: origosta pisteeseen 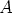 osoittava vektori lisättynä
60 astetta kierretyllä vektorilla
osoittava vektori lisättynä
60 astetta kierretyllä vektorilla 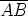 . Vastaavasti
. Vastaavasti 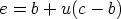 ja
ja
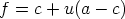 .
.
Koska kolmion keskijanojen leikkauspiste saadaan kärkipisteiden keskiarvona, on
![p = 1(a + b + d) = 1[2a + b + u(b- a)]
3 3](images/napoleon2x39x.gif) ja samoin
ja samoin ![q = 1[2b + c + u(c - b)]
3](images/napoleon2x40x.gif) ,
,
![r = 1[2c + a + u(a - c)]
3](images/napoleon2x41x.gif) .
.
Kolmion 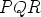 keskipiste on tällöin
keskipiste on tällöin
![1(p + q + r) = 1[2a + b + u(b- a) + 2b + c + u(c- b) + 2c + a + u(a - c)]
3 91
= 3(a + b + c),](images/napoleon2x43x.gif)
ts. sama kuin alkuperäisen kolmion keskijanojen leikkauspiste.
Kiertämällä vektoria 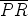 , ts. kertomalla erotuskompleksiluku
, ts. kertomalla erotuskompleksiluku 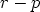 kiertotekijällä saadaan seuraavaa:
kiertotekijällä saadaan seuraavaa:
![u(r- p) = 1u[2c- a- b + u(2a - b- c)]
31 2
= 3[u(2c- a- b) + u (2a - b - c)]
= 13[u(2c- a- b) + (u - 1)(2a - b- c)]
1
= 3[b + c - 2a + u(a + c - 2b)]
= q- p.](images/napoleon2x46x.gif)
Tuloksena on siis vektori 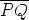 . Tällöin kulman
. Tällöin kulman 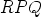 suuruus on 60 astetta ja
sivut
suuruus on 60 astetta ja
sivut 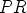 ja
ja 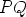 ovat yhtä pitkiä. Tämä riittääkin tekemään kolmion
ovat yhtä pitkiä. Tämä riittääkin tekemään kolmion 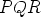 tasasivuiseksi.
tasasivuiseksi.
Todistus on valmis!
Linkkejä
Johdatus Napoleonin lauseeseen
Simo K. Kivelä 03.01.2005