Miksi kompleksilukuja?
Lukualueen vaiheittaisen laajentamisen luonnollisista luvuista kokonaislukujen ja
rationaalilukujen kautta reaalilukuihin (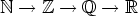 ) voidaan katsoa
syntyvän tarpeesta löytää ratkaisu yhä uusille yhtälötyypeille:
) voidaan katsoa
syntyvän tarpeesta löytää ratkaisu yhä uusille yhtälötyypeille: 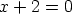 ei
ratkea luonnollisten lukujen joukossa, mutta kylläkin kokonaislukujen joukossa;
ei
ratkea luonnollisten lukujen joukossa, mutta kylläkin kokonaislukujen joukossa;
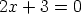 ei ratkea kokonaislukujen, mutta kyllä rationaalilukujen joukossa;
yhtälöllä
ei ratkea kokonaislukujen, mutta kyllä rationaalilukujen joukossa;
yhtälöllä 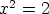 ei ole rationaalista ratkaisua, mutta reaalilukujoukkoon kuuluva
ratkaisu löytyy.
ei ole rationaalista ratkaisua, mutta reaalilukujoukkoon kuuluva
ratkaisu löytyy.
Samaa ajattelua voidaan yrittää jatkaa: Yhtälö 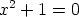 ei ratkea
reaalilukujoukossa, mutta voitaisiinko lukujoukkoa laajentaa siten, että sille
kuitenkin löytyisi ratkaisu?
ei ratkea
reaalilukujoukossa, mutta voitaisiinko lukujoukkoa laajentaa siten, että sille
kuitenkin löytyisi ratkaisu?
Suoraviivainen mahdollisuus on päättää ottaa käyttöön ’luku’ 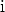 , jolla on
ominaisuus
, jolla on
ominaisuus 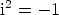 , ja sopia lisäksi, että sillä lasketaan reaalilukujen
laskusääntöjä noudattaen. Tällöin on
, ja sopia lisäksi, että sillä lasketaan reaalilukujen
laskusääntöjä noudattaen. Tällöin on 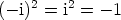 , ja yhtälölle
, ja yhtälölle 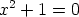 on saatu kaksi ratkaisua,
on saatu kaksi ratkaisua, 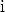 ja
ja 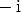 . Jotenkin luontevaa on tällöin myös
kirjoittaa
. Jotenkin luontevaa on tällöin myös
kirjoittaa 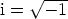 , vaikka tämä joissakin yhteyksissä osoittautuukin hieman
ongelmalliseksi.
, vaikka tämä joissakin yhteyksissä osoittautuukin hieman
ongelmalliseksi.
Edellä oleva jättää kuitenkin avoimeksi, mikä 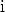 oikeastaan on ja voidaanko
ristiriitoihin joutumatta sopia, että sillä lasketaan reaalilukujen tapaan.
oikeastaan on ja voidaanko
ristiriitoihin joutumatta sopia, että sillä lasketaan reaalilukujen tapaan.
Kompleksiluvut määritelläänkin tämän takia hieman toisin ottamalla lähtökohdaksi
xy-taso  , jota ryhdytään kutsumaan kompleksitasoksi. Määrittelyprosessin
tuloksena saadaan kompleksilukualgebra, jossa neljä peruslaskutoimitusta
toimivat samoilla säännöillä kuin reaalilukualgebrassa. Lisäksi on voimassa
, jota ryhdytään kutsumaan kompleksitasoksi. Määrittelyprosessin
tuloksena saadaan kompleksilukualgebra, jossa neljä peruslaskutoimitusta
toimivat samoilla säännöillä kuin reaalilukualgebrassa. Lisäksi on voimassa
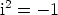 . (Kaikki aritmetiikka ei kuitenkaan toimi samoin kuin reaalialueella:
. (Kaikki aritmetiikka ei kuitenkaan toimi samoin kuin reaalialueella:
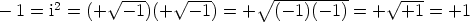 . Jokin
yhtäläisyysmerkeistä on ilmeisestikin väärä!)
. Jokin
yhtäläisyysmerkeistä on ilmeisestikin väärä!)
Kompleksiluvut osoittautuvat merkityksellisiksi monissa muissakin suhteissa kuin
polynomiyhtälöiden ratkaisemisessa. Niitä tarvitaan sekä monilla matematiikan
osa-alueilla että sovellettaessa matematiikkaa muissa tieteissä.
Linkkejä
Kompleksilukujen määrittely
Simo K. Kivelä 20.04.2005
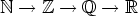 ) voidaan katsoa
syntyvän tarpeesta löytää ratkaisu yhä uusille yhtälötyypeille:
) voidaan katsoa
syntyvän tarpeesta löytää ratkaisu yhä uusille yhtälötyypeille: 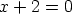 ei
ratkea luonnollisten lukujen joukossa, mutta kylläkin kokonaislukujen joukossa;
ei
ratkea luonnollisten lukujen joukossa, mutta kylläkin kokonaislukujen joukossa;
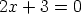 ei ratkea kokonaislukujen, mutta kyllä rationaalilukujen joukossa;
yhtälöllä
ei ratkea kokonaislukujen, mutta kyllä rationaalilukujen joukossa;
yhtälöllä 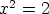 ei ole rationaalista ratkaisua, mutta reaalilukujoukkoon kuuluva
ratkaisu löytyy.
ei ole rationaalista ratkaisua, mutta reaalilukujoukkoon kuuluva
ratkaisu löytyy.
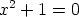 ei ratkea
reaalilukujoukossa, mutta voitaisiinko lukujoukkoa laajentaa siten, että sille
kuitenkin löytyisi ratkaisu?
ei ratkea
reaalilukujoukossa, mutta voitaisiinko lukujoukkoa laajentaa siten, että sille
kuitenkin löytyisi ratkaisu?
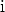 , jolla on
ominaisuus
, jolla on
ominaisuus 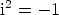 , ja sopia lisäksi, että sillä lasketaan reaalilukujen
laskusääntöjä noudattaen. Tällöin on
, ja sopia lisäksi, että sillä lasketaan reaalilukujen
laskusääntöjä noudattaen. Tällöin on 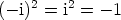 , ja yhtälölle
, ja yhtälölle 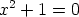 on saatu kaksi ratkaisua,
on saatu kaksi ratkaisua, 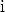 ja
ja 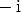 . Jotenkin luontevaa on tällöin myös
kirjoittaa
. Jotenkin luontevaa on tällöin myös
kirjoittaa 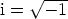 , vaikka tämä joissakin yhteyksissä osoittautuukin hieman
ongelmalliseksi.
, vaikka tämä joissakin yhteyksissä osoittautuukin hieman
ongelmalliseksi.
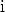 oikeastaan on ja voidaanko
ristiriitoihin joutumatta sopia, että sillä lasketaan reaalilukujen tapaan.
oikeastaan on ja voidaanko
ristiriitoihin joutumatta sopia, että sillä lasketaan reaalilukujen tapaan.
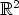 , jota ryhdytään kutsumaan
, jota ryhdytään kutsumaan 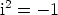 . (Kaikki aritmetiikka ei kuitenkaan toimi samoin kuin reaalialueella:
. (Kaikki aritmetiikka ei kuitenkaan toimi samoin kuin reaalialueella:
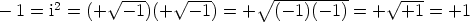 . Jokin
yhtäläisyysmerkeistä on ilmeisestikin väärä!)
. Jokin
yhtäläisyysmerkeistä on ilmeisestikin väärä!)