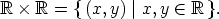
Lähtökohtana olkoon xy-taso, ts. joukko
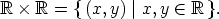
Tätä aletaan kutsua kompleksitasoksi tai kompleksilukujoukoksi ja sille käytetään
symbolia 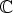 . Joukon alkioita merkitään lyhyesti
. Joukon alkioita merkitään lyhyesti 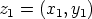 ,
, 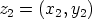 jne.
ja niitä kutsutaan kompleksiluvuiksi.
jne.
ja niitä kutsutaan kompleksiluvuiksi.
Joukon 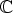 alkioille määritellään yhteenlasku ja kertolasku kaavoilla
alkioille määritellään yhteenlasku ja kertolasku kaavoilla
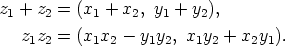
Esimerkiksi kompleksilukujen 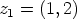 ja
ja  summa ja tulo ovat
siis
summa ja tulo ovat
siis
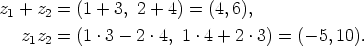
Osoittautuu, että kompleksiluvuilla, so. muotoa 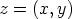 olevilla symboleilla
voidaan tällöin laskea samoilla säännöillä kuin reaaliluvuilla. Erityisesti on
olemassa kompleksiluvut nolla
olevilla symboleilla
voidaan tällöin laskea samoilla säännöillä kuin reaaliluvuilla. Erityisesti on
olemassa kompleksiluvut nolla 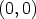 ja ykkönen
ja ykkönen 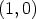 , jotka käyttäytyvät
kuten reaaliluvut
, jotka käyttäytyvät
kuten reaaliluvut 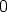 ja
ja 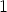 : nollan lisääminen toiseen kompleksilukuun ei muuta
sitä, toisen luvun kertominen ykkösellä ei muuta sitä.
: nollan lisääminen toiseen kompleksilukuun ei muuta
sitä, toisen luvun kertominen ykkösellä ei muuta sitä.
Jokaisella kompleksiluvulla 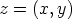 on vastaluku
on vastaluku 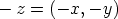 . Kun luku
ja vastaluku lasketaan yhteen, saadaan nolla
. Kun luku
ja vastaluku lasketaan yhteen, saadaan nolla 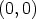 .
.
Jokaisella kompleksiluvulla 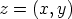 , joka poikkeaa nollasta, ts. ainakin toinen
luvuista
, joka poikkeaa nollasta, ts. ainakin toinen
luvuista  ja
ja 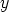 on
on 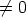 , on myös käänteisluku:
, on myös käänteisluku:
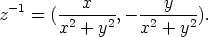
Luvun ja käänteisluvun tulo on ykkönen 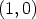 , kuten laskemalla voidaan
tarkistaa.
, kuten laskemalla voidaan
tarkistaa.
Erikoisasemassa osoittautuu olevan kompleksiluku 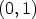 , jolle annetaan
nimeksi imaginaariyksikkö ja jolle käytetään symbolia
, jolle annetaan
nimeksi imaginaariyksikkö ja jolle käytetään symbolia 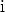 . Tämän tulo
itsensä kanssa, ts. toinen potenssi on kertolaskun määritelmän perusteella
. Tämän tulo
itsensä kanssa, ts. toinen potenssi on kertolaskun määritelmän perusteella
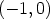 .
.
Linkkejä
Miksi kompleksilukuja?
Reaaliluvut kompleksilukujen osajoukkona
Kompleksilukujen kunta
Simo K. Kivelä 20.04.2005