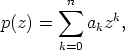
Kompleksikertoimiseksi polynomiksi kutsutaan lauseketta
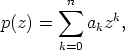
missä kertoimet 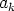 ovat kompleksilukuja. Muuttuja
ovat kompleksilukuja. Muuttuja  on luonnollisinta ajatella
kompleksiseksi. Kyseessä on siten funktio
on luonnollisinta ajatella
kompleksiseksi. Kyseessä on siten funktio  .
.
Vastaavasti puhutaan reaalikertoimisesta polynomista, jos kertoimet 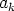 ovat reaalilukuja. Reaalikertoiminen polynomi on kompleksikertoimisen
erikoistapaus, ts. jokaista reaalikertoimista polynomia voidaan ajatella myös
kompleksikertoimisena. Muuttuja
ovat reaalilukuja. Reaalikertoiminen polynomi on kompleksikertoimisen
erikoistapaus, ts. jokaista reaalikertoimista polynomia voidaan ajatella myös
kompleksikertoimisena. Muuttuja  voidaan tällöin ajatella joko reaaliseksi tai
kompleksiseksi: kyseessä on funktio
voidaan tällöin ajatella joko reaaliseksi tai
kompleksiseksi: kyseessä on funktio 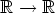 tai
tai 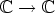 .
.
Jos 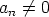 , on polynomin asteluku
, on polynomin asteluku 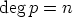 .
.
Algebran peruslauseen mukaan jokaisella vähintään ensimmäistä astetta
olevalla kompleksikertoimisella polynomilla 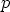 on ainakin yksi (reaalinen tai
kompleksinen) nollakohta, so. on olemassa
on ainakin yksi (reaalinen tai
kompleksinen) nollakohta, so. on olemassa 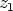 siten, että
siten, että 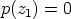 .
.
Algebran peruslause ei päde reaalialueella: esimerkiksi polynomilla 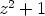 ei ole
lainkaan nollakohtia reaalilukujoukossa
ei ole
lainkaan nollakohtia reaalilukujoukossa 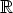 . Kompleksilukujoukko onkin siinä
mielessä reaalilukuja täydellisempi, että algebran peruslause saa yksinkertaisen
muodon.
. Kompleksilukujoukko onkin siinä
mielessä reaalilukuja täydellisempi, että algebran peruslause saa yksinkertaisen
muodon.
Algebran peruslause on luonnollisinta todistaa kompleksifunktioiden teorian pohjalta.
Linkkejä
Simo K. Kivelä 29.04.2005