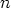 olevalla kompleksikertoimisella (tai reaalikertoimisella) polynomilla
olevalla kompleksikertoimisella (tai reaalikertoimisella) polynomilla
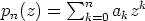 on algebran peruslauseen mukaan ainakin yksi (mahdollisesti
kompleksinen) nollakohta
on algebran peruslauseen mukaan ainakin yksi (mahdollisesti
kompleksinen) nollakohta 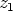 . Tällöin siis on
. Tällöin siis on 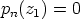 .
.
Astetta 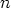 olevalla kompleksikertoimisella (tai reaalikertoimisella) polynomilla
olevalla kompleksikertoimisella (tai reaalikertoimisella) polynomilla
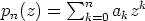 on algebran peruslauseen mukaan ainakin yksi (mahdollisesti
kompleksinen) nollakohta
on algebran peruslauseen mukaan ainakin yksi (mahdollisesti
kompleksinen) nollakohta 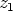 . Tällöin siis on
. Tällöin siis on 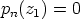 .
.
Jakolaskun 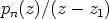 tuloksena saadaan osamäärä
tuloksena saadaan osamäärä 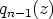 , joka on
, joka on
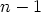 -asteinen polynomi, ja jakojäännös
-asteinen polynomi, ja jakojäännös 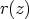 . Koska jakojäännös on alempaa
astetta kuin jakaja, on polynomin
. Koska jakojäännös on alempaa
astetta kuin jakaja, on polynomin 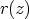 asteluku
asteluku 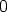 , ts. kyseessä on vakio:
, ts. kyseessä on vakio:
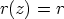 . Tällöin on
. Tällöin on
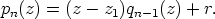
Sijoittamalla tähän 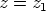 saadaan
saadaan 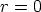 , jolloin
, jolloin
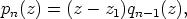
ts. polynomi 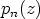 on jaollinen tekijällä
on jaollinen tekijällä 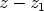 .
.
Askel voidaan toistaa: Jos 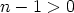 , polynomilla
, polynomilla 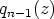 on nollakohta
on nollakohta 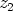 ja
ja
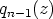 on jaollinen tekijällä
on jaollinen tekijällä 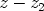 . Tällöin
. Tällöin 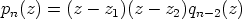 .
Näin voidaan jatkaa, kunnes päädytään yhtälöön
.
Näin voidaan jatkaa, kunnes päädytään yhtälöön
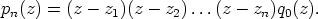
Polynomin 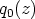 asteluku on
asteluku on 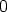 , joten kyseessä on vakio eikä algebran
peruslausetta enää voida soveltaa. Oikeanpuolen kertolasku osoittaa, että kyseessä
on potenssin
, joten kyseessä on vakio eikä algebran
peruslausetta enää voida soveltaa. Oikeanpuolen kertolasku osoittaa, että kyseessä
on potenssin 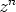 kerroin, ts.
kerroin, ts. 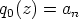 .
.
Siis:
Polynomi voidaan aina jakaa ensimmäistä astetta oleviin tekijöihin:
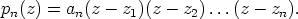
Luvut 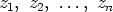 ovat polynomin
ovat polynomin 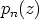 nollakohdat. Niiden joukossa
saattaa olla yhtä suuria ja reaalisenkin polynomin tapauksessa ne saattavat
kaikkikin olla kompleksisia. Jos yhtä suuret juuret lasketaan kertalukunsa
mukaisesti, ts. otetaan niin moneen kertaan kuin ne tekijöissä esiintyvät, voidaan
sanoa, että astetta
nollakohdat. Niiden joukossa
saattaa olla yhtä suuria ja reaalisenkin polynomin tapauksessa ne saattavat
kaikkikin olla kompleksisia. Jos yhtä suuret juuret lasketaan kertalukunsa
mukaisesti, ts. otetaan niin moneen kertaan kuin ne tekijöissä esiintyvät, voidaan
sanoa, että astetta 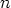 olevalla polynomilla on
olevalla polynomilla on 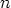 nollakohtaa.
nollakohtaa.
Tarkkoja arvoja polynomin nollakohdille ei aina voida löytää. Viidennen ja korkeampien asteiden polynomien nollakohdille ei ole olemassa yleisiä ratkaisukaavoja. Mielivaltaisen tarkkoja numeerisia approksimaatioita voidaan kyllä löytää.
Linkkejä
Polynomit, algebran peruslause
Reaalikertoimisen polynomin nollakohdat
Esimerkki polynomin tekijöihin jakamisesta
Neljännen asteen polynomin kuvaaja ja nollakohdat (interaktiivinen dokumentti)
Simo K. Kivelä 03.05.2005