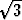Eulerin yhtälö

1) Toisen kertaluvun lineaarinen ja homogeeninen differentiaaliyhtälö x²y'' - 3xy' + y = 0 on esimerkki Eulerin yhtälöstä. Se on helpointa ratkaista yritteellä y = x^r. Tämän sijoittaminen yhtälöön antaa

r(r - 1)x^r - 3rx^r + x^r = 0.

Jakamalla tekijä x^r pois yhtälöstä päädytään ehtoon r² - 4r + 1 = 0, mistä seuraa r = 2 ± 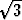. Yhtälön yleinen ratkaisu on siten

y = C₁x²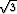⁺ + C₂x^2-.

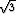Koska eksponentit eivät ole kokonaislukuja, on rajoituttava alueeseen x > 0.

2) Jos kolmannen kertaluvun yhtälöön x³y''' - 5x²y'' + 14xy' - 18y = 0 sijoitetaan yrite y = x^r , päädytään yhtälöön r³ - 8r² + 21r - 18 = 0. Tämän juuret ovat r₁ = 2, r₂ = r₃ = 3.

Tämä vastaa tilannetta, missä sijoituksella x = e^t vakiokertoimiseksi muunnetulla yhtälöllä on yleinen ratkaisu u = C₁e^2t + C₂e^3t + C₃te^3t. Sijoittamalla tähän t = ln x voidaan palata alkuperäiseen muuttujaan, ja yleiseksi ratkaisuksi saadaan

y = C₁x² + C₂x³ + C₃x³ ln x.

Edellytyksenä on, että x > 0.

Lukija todetkoon, että jos x < 0, niin yhtälön yleinen ratkaisu on

y = C₁x² + C₂x³ + C₃x³ ln(-x).

3) Jos yhtälöön x²y'' - 3xy' + 13y = 0 sijoitetaan yrite y = x^r, saadaan toisen asteen yhtälö r² - 4r + 13 = 0, jonka juuret ovat kompleksiset: r₁ = 2 + 3i, r₂ = 2 - 3i.

Vakiokertoimiseksi muunnetulla yhtälöllä on tällöin perusratkaisut u₁ = e^2t cos(3t) ja u₂ = e^2t sin(3t). Sijoittamalla näihin t = ln x saadaan perusratkaisuiksi y₁ = x² cos(3 ln x) ja y₂ = x² sin(3 ln x), jolloin yleinen ratkaisu on

y = C₁x² cos(3 ln x) + C₂x² sin(3 ln x),   x > 0.

Jos x < 0, on yleinen ratkaisu vastaavasti

y = C₁x² cos(3 ln(-x)) + C₂x² sin(3 ln(-x)).