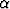 k + i
k + i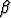 k, on syytä ensin lausua
eksponenttimuotoinen ratkaisu reaalimuodossa ja vasta tämän jälken sijoittaa
t = ln x:
k, on syytä ensin lausua
eksponenttimuotoinen ratkaisu reaalimuodossa ja vasta tämän jälken sijoittaa
t = ln x:
Lineaarista ja homogeenista differentiaaliyhtälöä
Pn(x)y(n) + Pn-1(x)y(n-1) + . . . + P1(x)y' + P0(x)y = 0
kutsutaan Eulerin yhtälöksi, jos kerroinfunktiot ovat muotoa Pk(x) = akxk, missä luvut ak ovat vakioita.
Tämä voidaan muuntaa vakiokertoimiseksi yhtälöksi sijoituksella x = et eli t = ln x. Tällöin on rajoituttava arvoihin x > 0. Tuntemattoman funktion y(x) sijaan tulee tällöin uusi tuntematon funktio u(t):
y(x) = y(et) = u(t).
Funktion u derivaatat ovat
| u'(t) | = y'(x)et, | ||
| u''(t) | = y''(x)(et)2 + y'(x)et, | ||
| u'''(t) | = y'''(x)(et)3 + 3y''(x)(et)2 + y'(x)et, | ||
| . . . |
| y(x) | = u(t), | ||
| y' (x) | = e-tu'(t) = x-1u'(t), | ||
| y'' (x) | = e-2t(u''(t) - u'(t)) = x-2(u''(t) - u'(t)), | ||
| y''' (x) | = e-3t(u'''(t) - 3u''(t) + 2u'(t)) = x-3(u'''(t) - 3u''(t) + 2u'(t)), | ||
| . . . |
y(x) = u(t) = u(ln x) = xrk
tai yhtyvien juurien tapauksessa y(x) = (ln x)pxrk.
Jos kerroin rk on kompleksinen, ts. rk = 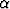 k + i
k + i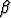 k, on syytä ensin lausua
eksponenttimuotoinen ratkaisu reaalimuodossa ja vasta tämän jälken sijoittaa
t = ln x:
k, on syytä ensin lausua
eksponenttimuotoinen ratkaisu reaalimuodossa ja vasta tämän jälken sijoittaa
t = ln x:
y(x) = u(t) = e kt[C1 cos(
kt[C1 cos(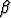 kt) + C2 sin(
kt) + C2 sin(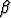 kt)] = x
kt)] = x k
[C1 cos(
k
[C1 cos(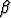 k ln x) + C2 sin(
k ln x) + C2 sin(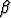 k ln x)].
k ln x)].
Eulerin yhtälö ratkaistaankin edellä sanottuun perustuen yleensä yritteellä y = xr, jolloin siirtymistä uuteen muuttujaan t ei tarvitse tehdä. Yritteen sijoittaminen yhtälöön antaa astetta n olevan polynomiyhtälön eksponentille r.