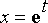Eulerin yhtälön muuntaminen vakiokertoimiseksi

Maple a voidaan käyttää yleisen Eulerin yhtälön muuntamiseen vakiokertoimiseksi yhtälöksi sijoituksella 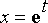. Seuraava esitys toimii periaatteessa mille tahansa kertaluvulle n . Jos n > 20, alkaa laskenta kuitenkin vaatia varsin paljon resursseja.

Syötetään Eulerin yhtälön kertaluku ja muodostetaan yhtälö:

> n:= 5;

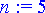
> euleryht:= sum(a[k]*x^k*(D@@k)(y)(x), k=0..n)=0;

Sijoituksen seurauksena syntyy uusi tuntematon funktio 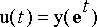. Funktiot y ja u toisiinsa sitova yhtälö talletetaan nimelle :

> yht[0]:= u(t)=y(exp(t));

Tätä yhtälöä derivoidaan muuttujan t suhteen n kertaa, jotta saadaan vastaavat derivaattojen väliset yhtälöt; nämä kerätään listaksi:

> yhtalot:= {seq(diff(yht[0], [t$k]), k=0..n)};

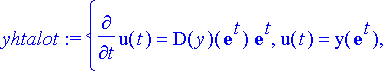
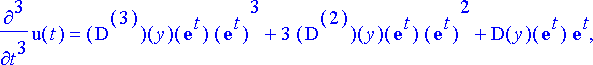
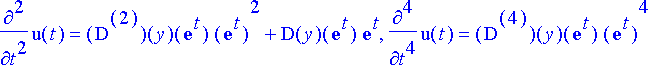
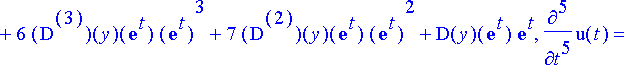
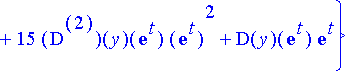
Tuntemattomat, ts. funktion y derivaatat kerätään omaksi listakseen; muuttujaksi otetaan t :

> tuntemattomat:= {seq((D@@k)(y)(exp(t)), k=0..n)};

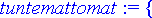
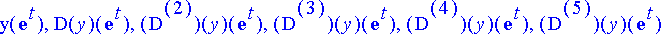
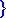
Jotta alkuperäinen differentiaaliyhtälö saadaan muunnetuksi funktiota u koskevaksi, yhtälöryhmästä ratkaistaan funktion y derivaatat ja sijoitetaan nämä differentiaaliyhtälöön; muuttujaksi otetaan t :

> sij:= solve(yhtalot, tuntemattomat);

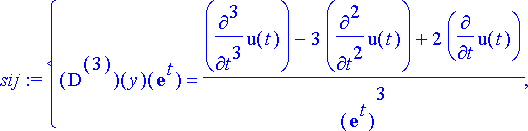
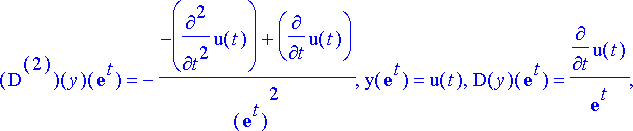
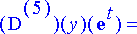
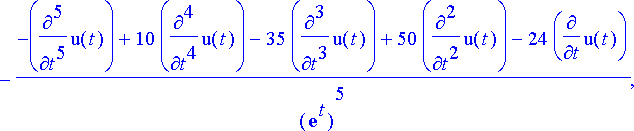
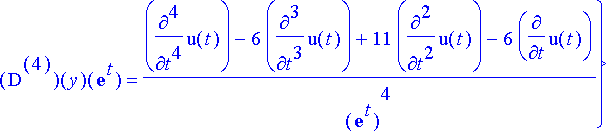
> subs(x=exp(t), euleryht):
vakiokertyht:= subs(sij, %):
simplify(%);

Tällöin on saatu Eulerin yhtälöä vastaava vakiokertoiminen yhtälö. Jotta tämä hahmottuisi selkeämmin, termit kootaan funktion u derivaattojen mukaan ryhmiteltyinä:

> derivaatat:=[seq(diff(u(t), [t$k]), k=0..n)];

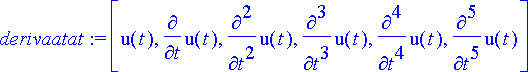
> ryhmitettyvakiokertyht:= collect(vakiokertyht, derivaatat);

Saadun yhtälön vasemmasta puolesta voidaan myös poimia eri derivaattojen kertoimet:

> coeffs(lhs(ryhmitettyvakiokertyht), derivaatat);

Kertoimet ovat todellakin vakioita.