| linkmp.mws |
Tarkastelun kohteena olkoon kertalukua
n
oleva vakiokertoiminen homogeeninen differentiaaliyhtälö:
> n:= 3;
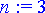
>
diffyht:= sum('a||k'*diff(y(x),[x$k]),k=0..n)=0;
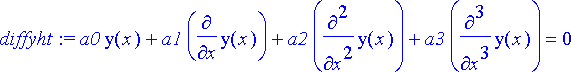
Karakteristinen yhtälö saadaan sijoittamalla yhtälöön yrite
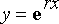 ja jakamalla sijoittamisen jälkeen eksponenttitekijä pois. Samaan tulokseen päästään korvaamalla differentiaaliyhtälössä derivaatat vastaavilla muuttujan
r
potensseilla:
ja jakamalla sijoittamisen jälkeen eksponenttitekijä pois. Samaan tulokseen päästään korvaamalla differentiaaliyhtälössä derivaatat vastaavilla muuttujan
r
potensseilla:
>
{seq(diff(y(x),[x$k])=r^k, k=0..n)}:
karaktyht:= subs(%,diffyht);
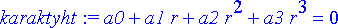
Kyseessä on polynomiyhtälö, jonka juuret
![r[1]](Images/linkmp5.gif) ,
,
![r[2]](Images/linkmp6.gif) jne. antavat differentiaaliyhtälön perusratkaisut
jne. antavat differentiaaliyhtälön perusratkaisut
![y = exp(r[1]*x)](Images/linkmp7.gif) ,
,
![y = exp(r[2]*x)](Images/linkmp8.gif) jne. Oletetaan, että yhtälöllä on kompleksinen juuripari
jne. Oletetaan, että yhtälöllä on kompleksinen juuripari
![r[1] = alpha+beta*I](Images/linkmp9.gif) ,
,
![r[2] = alpha-beta*I](Images/linkmp10.gif) , ja pyritään osoittamaan, että tällöin vastaaviksi perusratkaisuiksi kelpaavat
, ja pyritään osoittamaan, että tällöin vastaaviksi perusratkaisuiksi kelpaavat
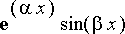 ja
ja
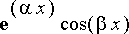 . Koska
. Koska
![r[1] = alpha+beta*I](Images/linkmp13.gif) ja
ja
![r[2] = alpha-beta*I](Images/linkmp14.gif) ovat juuria, seuraavat ehdot toteutuvat:
ovat juuria, seuraavat ehdot toteutuvat:
>
komplehdot:= {subs(r=alpha+I*beta,karaktyht), subs(r=alpha-I*beta,karaktyht)}:
simplify(%);
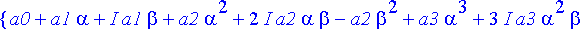
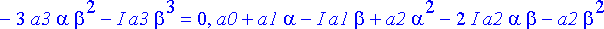
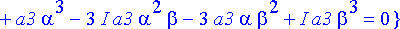
Yhtälöissä esiintyvät vakiot ovat kaikki reaalisia, jolloin periaatteessa kahdesta kompleksisesta ehdosta saadaan neljä reaalista ehtoa asettamalla kummankin reaali- ja imaginaariosa erikseen =0. Erilaisia ehtoja saadaan kuitenkin vain kaksi, kuten pitääkin: Jos nimittäin reaalikertoimisella polynomiyhtälöllä on juurena
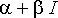 , myös liittoluku on juuri.
, myös liittoluku on juuri.
Imaginaariluvun reaaliosa ja imaginaariosa saadaan poimittua komennoilla Re ja Im . Koska Maple ei tiedä ovatko muuttujat reaalisia vai kompleksisia, on sievennyskomennon simplify yhteydessä käytettävä parametria assume=real , joka määrittää muuttujat reaalisiksi.
>
{Re(lhs((komplehdot[1])))=0,Im(lhs((komplehdot[1])))=0}:
ehdot:= simplify(%,assume=real);
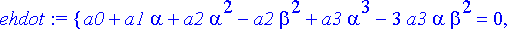
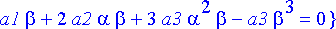
Sijoitetaan tutkittavat perusratkaisut differentiaaliyhtälöön:
>
sij:=
{algsubs(y(x)=exp(alpha*x)*sin(beta*x),diffyht), algsubs(y(x)=exp(alpha*x)*cos(beta*x),diffyht)}:simplify(%);
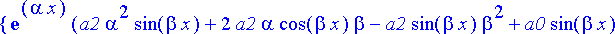
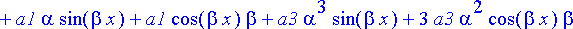
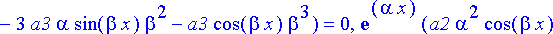
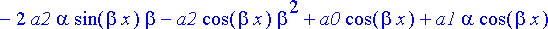
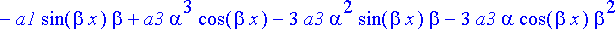
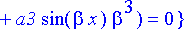
Ongelmana on, toteutuvatko nämä yhtälöt, kun oletetaan, että
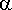 ja
ja
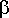 toteuttavat edellä johdetut ehdot:
toteuttavat edellä johdetut ehdot:
> simplify(sij,ehdot);

Yhälöt näyttävät olevan tosia, ja vastaavat perusratkaisut siis todella ovat
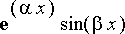 ja
ja
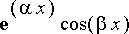 .
.
Symbolisissa laskentajärjestelmissä kuten
Maple
ssa on suhteellisen hyvät työkalut (usean muuttujan) polynomiehtojen käsittelyyn; taustalla ovat ns.
Gröbnerin kannat
. Probleeman monimutkaistuessa laskennan raskaus kuitenkin kasvaa nopeasti.
Kompleksisten juurten tapausta voidaan käsitellä myös toisin. Koska kompleksiluvut toteuttavat samanlaiset laskusäännöt (derivointisäännöt mukaanluettuina) kuin reaaliluvutkin, voidaan ajatella, että kirjoitetaan differentiaaliyhtälön yleinen ratkaisu kompleksisten eksponenttifunktioiden avulla:
> komplratk:= _C1*exp((alpha+I*beta)*x)+_C2*exp((alpha-I*beta)*x);
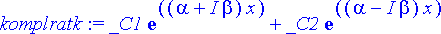
Tämä kehitetään käyttäen eksponenttifunktion laskusääntöä
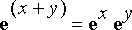 , joka on voimassa myös kompleksitapauksessa, ja sen jälkeen sovelletaan
Eulerin kaavaa
, joka on voimassa myös kompleksitapauksessa, ja sen jälkeen sovelletaan
Eulerin kaavaa
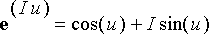 . Laskun voi tehdä käsin tai käyttämällä sopivasti
Maple
n komentoja.
. Laskun voi tehdä käsin tai käyttämällä sopivasti
Maple
n komentoja.
Convert
-komento muuntaa lausekkeen kaikki exponenttimerkinnät trigonometrisiksi. Koska emme kuitenkaan halua muuntaa termejä, jotka sisältävät
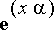 trigonometrisiksi, on tehtävä muunnos takaisin eksponenttimuotoon.
trigonometrisiksi, on tehtävä muunnos takaisin eksponenttimuotoon.
>
convert(komplratk,trig):
trigratk:= subs(convert(exp(x*alpha),trig)=exp(x*alpha),%):
expand(%);
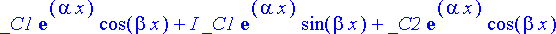
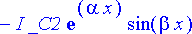
Tämä todellakin näyttää sisältävän haluttua muotoa
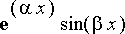 ja
ja
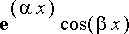 olevia termejä. Näiden kertoimet ovat
olevia termejä. Näiden kertoimet ovat
>
coeff(trigratk,sin(beta*x)):
sinkerroin:=coeff(%,exp(alpha*x));
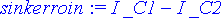
>
coeff(trigratk,cos(beta*x)):
coskerroin:=coeff(%,exp(alpha*x));
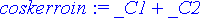
Ratkaisu voidaan sieventää antamalla näille kertoimille nimet _C3 ja _C4 :
> simplify(trigratk,{sinkerroin=_C3,coskerroin=_C4});
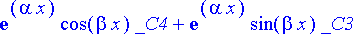
_C1 ja _C2 sekä toisaalta _C3 ja _C4 ovat symmetrisessä asemassa. Jos kumpi tahansa pari valitaan mielivaltaisesti, toinen pari määräytyy.