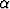 + i
+ i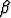 ,
r2 =
,
r2 = 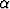 - i
- i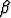 . Vastaavat perusratkaisut voitaisiin kirjoittaa kompleksisen eksponenttifunktion
avulla muodossa
. Vastaavat perusratkaisut voitaisiin kirjoittaa kompleksisen eksponenttifunktion
avulla muodossa
Kertalukua n oleva lineaarinen vakiokertoiminen homogeeninen differentiaaliyhtälö on
y(n) + an-1y(n-1) + . . . + a1y' + a0y = 0,
missä kertoimet ak ovat vakioita. Yleisen lineaariyhtälöiden teorian mukaan tämän ratkaisu on muotoa
y = C1y1(x) + C2y2(x) + . . . + Cnyn(x),
missä funktiot yk ovat lineaarisesti riippumattomia.
Yhtälö voidaan ratkaista yritteellä y = erx, missä luku r määrätään siten, että yrite toteuttaa yhtälön. Yritteen derivaatat ovat yksinkertaisia: y(k) = rkerx. Kun nämä sijoitetaan differentiaaliyhtälöön, saadaan
(rn + an-1rn-1 + . . . + a1r + a0)erx = 0.
Tekijä erx voidaan jakaa pois, ja päädytään polynomiyhtälöön, ns. karakteristiseen yhtälöön
rn + an-1rn-1 + . . . + a1r + a0 = 0.
Jos tämän juuret r1, r2, . . . , rn ovat kaikki reaalisia ja eri suuria, on löydetty lineaarisesti riippumattomat perusratkaisut:
y1(x) = er1x, y2(x) = er2x, . . . , yn(x) = ernx.
Jos joukossa on yhtä suuria juuria, ei perusratkaisuihin voida ottaa kahteen kertaan samaa funktiota, koska tällöin systeemistä tulisi lineaarisesti riippuva. Voidaan osoittaa, että kahden yhtä suuren juuren (r1 = r2 = r) tapauksessa vastaaviksi lineaarisesti riippumattomiksi perusratkaisuiksi kelpaavat y1(x) = erx ja y2 (x) = xerx. Jos yhtä suuria juuria on enemmän, vastaaviin lineaarisesti riippumattomiin ratkaisuihin tulee korkeampia muuttujan x potensseja: y3(x) = x2erx jne.
Jos juurten joukossa on kompleksilukuja, nämä esiintyvät liittolukupareina: r1 = 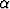 + i
+ i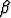 ,
r2 =
,
r2 = 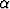 - i
- i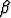 . Vastaavat perusratkaisut voitaisiin kirjoittaa kompleksisen eksponenttifunktion
avulla muodossa
. Vastaavat perusratkaisut voitaisiin kirjoittaa kompleksisen eksponenttifunktion
avulla muodossa
y1(x) = e( +i
+i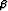 )x, y2(x) = e(
)x, y2(x) = e( -i
-i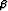 )x,
)x,
mutta koska differentiaaliyhtälö on reaalinen, on luontevampaa käyttää reaalisia perusratkaisuja. Eulerin kaavan eit = cos t + i sin t avulla voidaan kompleksisten eksponenttifunktioiden avulla lausutut ratkaisut muuntaa reaaliseen muotoon, jossa lineaarisesti riippumattomina funktioina ovat
y1(x) = e x sin(
x sin(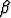 x), y2(x) = e
x), y2(x) = e x cos(
x cos(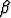 x).
x).