Differentiaaliyhtälön ratkaisun sijoittaminen yhtälöön

Olkoon tarkastelun kohteena differentiaaliyhtälö

> diffyht:= diff(y(x), x, x)-4*diff(y(x), x)+13*y(x)=0;

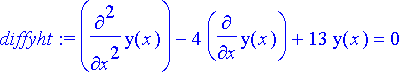
jonka lausekemuotoinen ratkaisu on

> y0:= dsolve(diffyht, y(x));

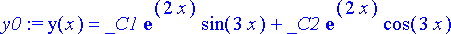
Kyseessä on ratkaisufunktiota y( x ) koskeva sijoitussääntö. Vastaavat sijoitussäännöt derivaatoille saadaan tätä derivoimalla:

> y1:= diff(y0, x);

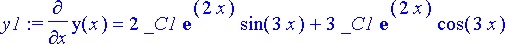
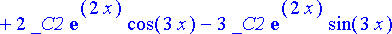
> y2:= diff(y0, x, x);

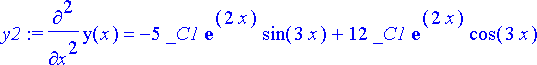
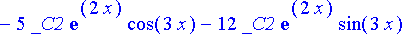
Kerätään sijoitussäännöt joukoksi ja sijoitetaan yhtälöön:

> sijoitus1:= subs({y1, y2, y0}, diffyht);

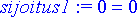
Tuloksesta nähdään, että yhtälö toteutuu.

Algebrallinen sijoitus

Helpommalla päästään, jos tehdään tavallisen sijoituksen ( subs ) sijasta algebrallinen sijoitus ( algsubs ). Tällöin Maple tekee automaattisesti derivoinnit.

> sijoitus2:= algsubs(y0, diffyht);

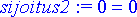
Tuloksesta nähdään jälleen, että yhtälö toteutuu.