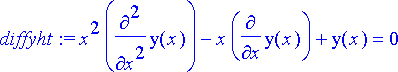
| symalg.mws |
Maplessa on käytettävissä differentiaaliyhtälöiden ratkaisemiseen komento
dsolve
. Tämä saa kaksi argumenttia: ratkaistava yhtälö ja tuntematon funktio. Suositeltava käytäntö on tallettaa yhtälö aluksi jollekin nimelle ja käyttää tätä
dsolve
-komennon argumenttina:
> diffyht:= x^2*diff(y(x), x, x)-x*diff(y(x), x)+y(x)=0;
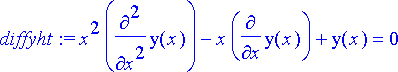
> ratkaisu:= dsolve(diffyht, y(x));
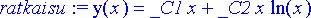
Yhtälön voi luonnollisesti kirjoittaa dsolve -komentoon suoraankin:
> ratkaisu:= dsolve(x^2*diff(y(x), x, x)-x*diff(y(x), x)+y(x)=0, y(x));
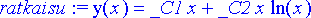
Ratkaisu antaa funktion y( x ) lausekkeen sijoitussäännön muodossa joukkona. Kukin joukon alkio on jokin yhtälön ratkaisuksi kelpaava lauseke. Tässä ratkaisulausekkeita on kuitenkin vain yksi, yhtälön yleinen ratkaisu. Määräämättömät vakiot ovat muodossa _ C1 , _ C2 jne.
Jotta ratkaisun lauseketta voitaisiin helposti käyttää, se kannattaa tallettaa jollekin nimelle:
> yleinenratkaisu:= subs(ratkaisu, y(x));
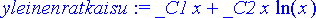
(Lausekkeeseen y(
x
) siis tehdään ratkaisun antaman sijoitussäännön mukainen sijoitus ja tulos talletetaan nimelle
yleinenratkaisu
.)
Tästä saadaan yksittäisratkaisu sijoittamalla vakioille jotkin arvot, minkä jälkeen voidaan vaikkapa piirtää kuvaaja:
> yksittaisratkaisu:= subs({_C1=2, _C2=-1}, yleinenratkaisu);
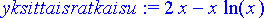
> plot(yksittaisratkaisu, x=0.1..5);
![[Maple Plot]](Images/symalg6.gif)
Ratkaisu voidaan myös määritellä funktioksi, jolloin sitä voidaan käyttää kuten mitä tahansa funktiota.
> yr:= unapply(yleinenratkaisu, x);
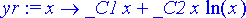
> yr(t);
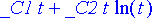
> yr(2);
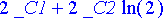
> diff(yr(t), t);
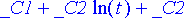
Komennolla dsolve voidaan myös ratkaista alkuarvoprobleema, jolloin differentiaaliyhtälö ja alkuehdot on annettava joukkona.
> ratkaisu:= dsolve({diffyht, y(1)=2, D(y)(1)=5}, y(x));
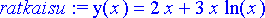
Dsolve -komennon ensimmäisenä argumenttina voi olla myös useamman differentiaaliyhtälön ja mahdollisten alkuehtojen muodostama joukko, jolloin sitä voidaan käyttää yhtälöryhmien ratkaisemiseen. Toisessa argumentissa tulee tällöin olla tuntemattomien funktioiden muodostama joukko.
> ratkaisu:= dsolve({diff(x(t), t)=4*x(t)-2*y(t), diff(y(t), t)=x(t)+y(t), x(0)=3, y(0)=2}, {x(t), y(t)});
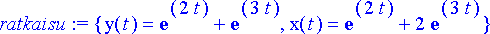
DSolve
-komento ei onnistu ratkaisemaan läheskään kaikkia differentiaaliyhtälöitä; kaikkihan eivät ole alkeisfunktioiden tai edes ns. erikoisfunktioiden avulla ratkaistavissakaan. Se ei kuitenkaan ratkaise edes kaikkia sellaisia, jotka ovat käsin laskemalla suhteellisen helposti ratkaistavissa. Toisaalta työläissä tehtävissä se on korvaamaton apuväline.
Differentiaaliyhtälöiden ratkaiseminen on vaikea tehtävä ja tietokonealgebrassa käytetyistä algoritmeista tulee herkästi monimutkaisia. Tällaisina ne ovat myös alttiita virheille eikä tuloksiin siten pidä sokeasti luottaa. Ohjelmistot kehittyvät versio versiolta. Uudempi versio ratkaisee yleensä aina useampia yhtälöitä kuin edellinen — ja tekee virheitä eri paikoissa kuin edellinen.
Dsolve-komennon toimintaa ratkaisun aikana on mahdollista seurata komennolla infolevel[dsolve]:=3 . Oletusarvoisesti infolevel -arvo on 0 . Vastaavasti voidaan seurata myös minkä tahansa muun komennon toimintaa.