Toisen tai korkeamman kertaluvun yhtälön muuntaminen normaaliryhmäksi

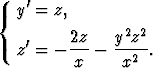
1) Toisen kertaluvun differentiaaliyhtälöä

x²y'' + 2xy' + y'²y² = 0

vastaava normaaliryhmä muodostetaan seuraavasti: Otetaan käyttöön uusi tuntematon funktio z = y' ; tällöin y'' = z'. Differentiaaliyhtälö saa nyt muodon

x²z' + 2xz + z²y² = 0.

Normaaliryhmässä on kaksi tuntematonta funktiota, y ja z; ryhmän yhtälöt esittävät näiden derivaatat funktioiden ja muuttujan x avulla:

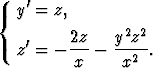
2) Neljännen kertaluvun yhtälöä y'''' + xy = 0 vastaavaa normaaliryhmää muodostettaessa uusiksi tuntemattomiksi funktioiksi otetaan funktion y derivaatat kolmanteen kertalukuun saakka: u = y', v = y'', w = y'''. Tällöin y' = u, u' = y'' = v, v' = y''' = w ja differentiaaliyhtälön mukaan w' = y'''' = -xy.

Normaaliryhmä on siten

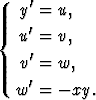
Ryhmä voidaan kirjoittaa vektorimuotoon merkitsemällä

Y =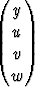

ja määrittelemällä vektoriarvoinen funktio F yhtälöllä

F (x, Y ) = .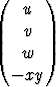

Tällöin normaaliryhmä vastaa vektoriyhtälöä

Y ' = F (x, Y ).