Normaaliryhmä

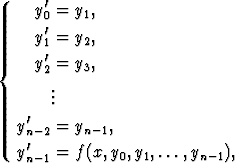
Kertalukua n oleva differentiaaliyhtälö

y⁽ⁿ⁾ = f(x, y, y', . . . , y^(n-1))

voidaan kirjoittaa ensimmäisen kertaluvun differentiaaliyhtälöryhmäksi, ns. normaaliryhmäksi, jossa on n tuntematonta funktiota ja n yhtälöä. Etuna on, että tällöin kyseessä on ensimmäisen kertaluvun yhtälöt, mutta haittana, että näitä on useita.

Uusiksi tuntemattomiksi funktioiksi otetaan funktion y lisäksi sen derivaatat kertalukuun n - 1 saakka:

y₀ = y,   y₁ = y',   y₂ = y'',   . . .   y_n-2 = y^(n-2),   y_n-1 = y^(n-1).

Tällöin on

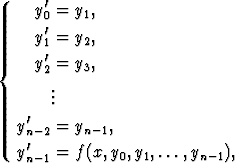
missä viimeinen yhtälö on itse asiassa alkuperäinen differentiaaliyhtälö. Kyseessä on alkuperäistä differentiaaliyhtälöä vastaava normaaliryhmä.

Saatu normaaliryhmä voidaan kirjoittaa tiiviimpään vektorimuotoon kokoamalla tuntemattomat funktiot n-komponenttiseksi vektoriksi Y ja määrittelemällä funktio F , jonka arvot ovat n-komponenttisia vektoreita:

Y = ,     F (x, Y ) = .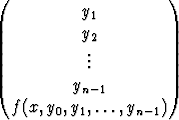

Normaaliryhmä voidaan tällöin kirjoittaa lyhyesti vektorimuotoon

Y ' = F (x, Y ),

missä derivaatta Y ' lasketaan komponenteittain. Ryhmä on tällöin muodoltaan samanlainen kuin tavallinen ensimmäisen kertaluvun differentiaaliyhtälö. Erona on, että funktio F onkin vektoriarvoinen ja tuntematon funktio Y on myös vektori.

Vektorimuodon käyttökelpoisuus perustuu siihen, että monet ensimmäisen kertaluvun yhtälöä koskevat algoritmit voidaan yleistää korkeampia kertalukuja koskeviksi, kun niitä sovelletaan vektorimuotoon.