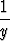
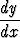 = x,
= x,
Koska differentiaaliyhtälö y' = xy voidaan kirjoittaa muotoon
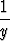
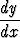 = x,
= x,
se on separoituva, ja ratkaisu saadaan muodossa
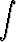
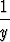 dy =
dy = 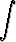 x dx + C.
x dx + C.
Integroinnit antavat
ln|y| = 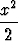 + C,
+ C,
jolloin
y = ±eCex2/2 = C1ex2/2,
missä on merkitty C1 = ±eC.
Tähän muotoon päästään suoraankin kirjoittamalla integroinnissa vakio muotoon ln|C|:
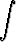 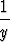 dy = dy = 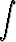 x dx + ln|C|, x dx + ln|C|, | |||
| ln|y| = x2/2 + ln|C|, | |||
| |y| = |C|ex2/2, | |||
| y = Cex2/2. |
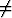 0.
Jos C = 0, saadaan yksittäisratkaisuksi y(x) = 0. Tämä on alkuperäisen yhtälön ratkaisu,
mutta ei separoituun muotoon kirjoitetun yhtälön ratkaisu nimittäjän nollaksi
tulemisen takia. Tämän johdosta arvo C = 0 on erikoistapaus ratkaisuprosessin
kannalta.
0.
Jos C = 0, saadaan yksittäisratkaisuksi y(x) = 0. Tämä on alkuperäisen yhtälön ratkaisu,
mutta ei separoituun muotoon kirjoitetun yhtälön ratkaisu nimittäjän nollaksi
tulemisen takia. Tämän johdosta arvo C = 0 on erikoistapaus ratkaisuprosessin
kannalta.