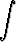 f(y(x))y'(x) dx =
f(y(x))y'(x) dx = 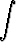 g(x) dx + C,
g(x) dx + C,
Ensimmäisen kertaluvun differentiaaliyhtälö on separoituva, jos se voidaan kirjoittaa muotoon f(y)y' = g(x) eli
f(y(x))y'(x) = g(x),
missä f ja g ovat tarkastelualueessa määriteltyjä integroituvia funktioita.
Integroimalla puolittain muuttujan x suhteen saadaan
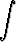 f(y(x))y'(x) dx =
f(y(x))y'(x) dx = 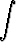 g(x) dx + C,
g(x) dx + C,
missä C on integroimisvakio. Sijoittamalla vasemman puolen integraalissa y = y(x), jolloin dy = y' (x) dx, saadaan
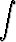 f(y) dy =
f(y) dy = 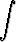 g(x) dx + C.
g(x) dx + C.
Tähän muotoon päästään muistisäännönomaisesti suoraankin käyttämällä derivaatalle
Leibnizin merkintää y' = 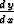 , jolloin yhtälö saa muodon
, jolloin yhtälö saa muodon
f(y)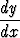 = g(x).
= g(x).
Laskemalla Leibnizin symbolilla kuin millä tahansa osamäärällä saadaan separoitu muoto f(y) dy = g(x) dx, missä muuttujat on eroteltu eri puolille yhtäläisyysmerkkiä. Tämä integroidaan puolittain.
Mikäli funktioiden f ja g integraalifunktiot F ja G ovat löydettävissä, päädytään muotoon
F (y) = G(x) + C.
Tämä on differentiaaliyhtälön ratkaisu implisiittisessä muodossa, ts. muodossa, joka ei suoraan anna funktiota y(x). Ratkaisemalla saatu yhtälö y:n suhteen — jos mahdollista — löydetään myös funktion y lauseke.
Menettelyn periaatteellisena edellytyksenä on, että ratkaisu y(x) on tarkastelualueessa olemassa. Muutoin ei integroimismuuttujan vaihtoa y = y(x) voida vasemman puolen integraalissa tehdä. Käytännössä tähän ei yleensä kiinnitetä huomiota: ratkaisun olemassaolo voidaan jälkikäteen tarkistaa sijoittamalla funktio y suoraan alkuperäiseen yhtälöön.