Sarjaratkaisun etsiminen Maplella

Esimerkit : Sarjaratkaisut

Sarjaratkaisun etsiminen Maplella

Olkoon tarkasteltavana ensimmäisen kertaluvun differentiaaliyhtälö:

> diffyht:= diff(y(x), x)=1+y(x)^2;

diffyht := diff(y(x),x) = 1+y(x)^2

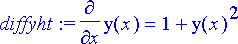
Tälle pyritään etsimään sarjaratkaisu origokeskisenä potenssisarjana. Tavoitteena on laskea sarjan termien kertoimet n -asteiseen termiin saakka:

> n:= 10;

n := 10

Potenssisarjojen käsittelyä varten on Maple ssa paketti powseries .

> with(powseries):

Tarvittava potenssisarjamuotoinen yrite on

> powcreate(yrite(k)=a[k]):
tpsform(yrite, x, n);

series(a[0]+a[1]*x+a[2]*x^2+a[3]*x^3+a[4]*x^4+a[5]*...

Powcreate -komennolla luodaan Maple -proseduuri, joka vastaa haluttua potenssisarjaa. Tpsform -komennolla saadaan tulostettua haluttu määrä termejä luodusta potenssisarjasta. Powseries -pakettia käytettäessä on potenssisarjojen väliset operaatiot tehtävä paketin työkaluilla. Esimerkiksi kahta powcreate -komennolla luotua potenssisarjaa ei voida kertoa keskenään operaattorilla *, vaan on käytettävä paketin komentoa multiply . Vastaavasti diff -komento ei pure potenssisarjaan vaan on käytettävä komentoa powdiff .

Sijoittamista varten on paketin työkaluilla laskettava valmiiksi alkuperäisessä differentiaaliyhtälössä esiintyvät derivointi ja toiseen potenssiin korottaminen. Tämän jälkeen potenssisarjoista muodostetaan sijoitusta varten polynomit ottamalla mukaan n ensimmäistä termiä.

> yriteder:= powdiff(yrite):
tpsform(yriteder, x, n);

series(a[1]+2*a[2]*x+3*a[3]*x^2+4*a[4]*x^3+5*a[5]*x...

> yritetoiseen:= multiply(yrite, yrite):
tpsform(yritetoiseen, x, n);

series(a[0]^2+2*a[0]*a[1]*x+(2*a[0]*a[2]+a[1]^2)*x^...

> yritederpol:= convert(tpsform(yriteder, x, n), polynom);

yritederpol := a[1]+2*a[2]*x+3*a[3]*x^2+4*a[4]*x^3+...

> yritetoiseenpol:= convert(tpsform(yritetoiseen, x, n), polynom);

yritetoiseenpol := a[0]^2+2*a[0]*a[1]*x+(2*a[0]*a[2...

Sijoitetaan yrite differentiaaliyhtälöön.

> sarjayht:= yritederpol=1+yritetoiseenpol;

sarjayht := a[1]+2*a[2]*x+3*a[3]*x^2+4*a[4]*x^3+5*a...

Yhtälön oikealla ja vasemmalla puolella on potenssisarja. Jotta nämä olisivat samat, tulee samakorkuisten potenssien kertoimien yhtälön oikealla ja vasemmalla puolella olla samat. Vähentämällä yhtälön oikea puoli vasemmasta saadaan aikaan polynomi, jonka potenssien kertoimien tulee tällöin olla 0. Poimimalla kertoimet coeffs -komennolla ja määrittelemällä ne nollaksi, saadaan yhtälöryhmä.

> lhs(sarjayht)-rhs(sarjayht):
coeffs(%, x):
yhtalot:= {seq(%[i]=0, i=1..n)};

$yhtalot := {a[1]-1-a[0]^2 = 0, 2*a[2]-2*a[0]*a[1] =...$
$yhtalot := {a[1]-1-a[0]^2 = 0, 2*a[2]-2*a[0]*a[1] =...$
$yhtalot := {a[1]-1-a[0]^2 = 0, 2*a[2]-2*a[0]*a[1] =...$
$yhtalot := {a[1]-1-a[0]^2 = 0, 2*a[2]-2*a[0]*a[1] =...$
$yhtalot := {a[1]-1-a[0]^2 = 0, 2*a[2]-2*a[0]*a[1] =...$
$yhtalot := {a[1]-1-a[0]^2 = 0, 2*a[2]-2*a[0]*a[1] =...$
$yhtalot := {a[1]-1-a[0]^2 = 0, 2*a[2]-2*a[0]*a[1] =...$

Tuloksena on rekursiivinen epälineaarinen yhtälöryhmä: ensimmäisestä yhtälöstä voidaan ratkaista a[1] , jos a[0] tunnetaan, toisesta tämän jälkeen a[2] , kolmannesta a[3] jne. Kokonaisuudessaan ryhmä voidaan ratkaista solve -komennolla. Tässä jälkimmäiseksi argumentiksi pitäisi oikeastaan antaa lista yhtälöryhmän tuntemattomista, mutta oletuksena on, että ratkaisu tapahtuu kaikkien ryhmässä esiintyvien symbolien suhteen. Kaikkia tuntemattomia ei saada ratkaistuiksi, vaan muut voidaan ainoastaan lausua ensimmäisen kertoimen a[0] avulla.

> ratk:= solve(yhtalot);

$ratk := {a[1] = 1+a[0]^2, a[3] = 4/3*a[0]^2+a[0]^4+...$
$ratk := {a[1] = 1+a[0]^2, a[3] = 4/3*a[0]^2+a[0]^4+...$
$ratk := {a[1] = 1+a[0]^2, a[3] = 4/3*a[0]^2+a[0]^4+...$
$ratk := {a[1] = 1+a[0]^2, a[3] = 4/3*a[0]^2+a[0]^4+...$
$ratk := {a[1] = 1+a[0]^2, a[3] = 4/3*a[0]^2+a[0]^4+...$
$ratk := {a[1] = 1+a[0]^2, a[3] = 4/3*a[0]^2+a[0]^4+...$
$ratk := {a[1] = 1+a[0]^2, a[3] = 4/3*a[0]^2+a[0]^4+...$

Sijoittamalla kertoimet yritteeseen saadaan ratkaisuna olevan potenssisarjan alkupää:

> sarjaratk:= subs(ratk, tpsform(yrite, x, n+1));

sarjaratk := series(a[0]+(1+a[0]^2)*x+a[0]*(1+a[0]^...

Tämä sisältää yhden määräämättömän vakion a[0] , kuten ensimmäisen kertaluvun differentiaaliyhtälön yleiselle ratkaisulle luonnollista onkin. Jos alkuehdoksi valitaan y (0) = 0, tulee olla a[0] = 0 . Vastaava yksittäisratkaisu on

> yksratk:= subs(a[0]=0, sarjaratk);

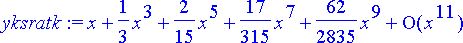
yksratk := series(1*x+1/3*x^3+2/15*x^5+17/315*x^7+6...

Tämä on sama kuin funktion tan( x ) origokeskinen Taylorin sarja:

> series(tan(x), x, n+1);

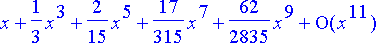
series(1*x+1/3*x^3+2/15*x^5+17/315*x^7+62/2835*x^9+...

Näin tulee ollakin, sillä differentiaaliyhtälö on separoituva ja sen yleiseksi ratkaisuksi saadaan y = tan( x + C ).

> dsolve(diffyht, y(x));

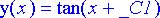
y(x) = tan(x+_C1)

Jotta sarjaratkaisulle voitaisiin piirtää kuvaaja, siitä on pudotettava jäännöstermi pois. Tämän tarkkaa lausekettahan ei tunneta eikä sille siis voida laskea numeerisia arvoja piirtämistä varten. Jäännöstermin poistaminen tapahtuu muuntamalla potenssisarja polynomiksi komennolla convert .

> poly:= convert(yksratk, polynom);

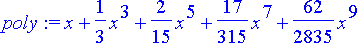
poly := x+1/3*x^3+2/15*x^5+17/315*x^7+62/2835*x^9

Sarjaratkaisu ja funktio tan( x ) samassa kuvassa:

> plot({poly, tan(x)}, x=0..1.5);

[Maple Plot]

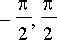Esitetty lasku ei anna viitteitä sarjaratkaisun suppenemisalueesta. Kokonaan muilla keinoilla voidaan osoittaa, että tangentin origokeskisen Taylorin sarjan suppenemissäde on pi/2 . Sarja suppenee siis vain välillä ] -pi/2, pi/2 [.

Haluttua termilukua voidaan edellä olevassa laskussa muuttaa ja tämän jälkeen laskea kaikki uudelleen valinnalla Evaluate Notebook valikosta Kernel/Evaluation.

Ratkaisu suoraan dsolve-komennolla

Maple n dsolve -komennolla on mahdollista laskea suoraan ratkaisuja, jotka ovat Taylorin sarjoja. Tällöin käytetään parametria type=series .

Esimerkkinä edellä johdettu sarjaratkaisu suoraan dsolve -komennolla:

> Order:=10:
dsolve({diffyht, y(0)=0}, y(x), type=series):
simplify(%);

y(x) = series(1*x+1/3*x^3+2/15*x^5+17/315*x^7+62/28...

Ratkaiseminen: sarjamuotoinen yrite

SKK & MS 31.05.2001