 ak(x - x0)k,
ak(x - x0)k,
Differentiaaliyhtälölle voidaan myös etsiä ratkaisua sarjamuodossa. Yritteeksi valitaan tällöin potenssisarja, jonka kehityskeskuksena on se piste x0, jossa alkuehto annetaan. Yrite on tällöin muotoa
y =  ak(x - x0)k,
ak(x - x0)k,
ja tavoitteena on määrittää kertoimet ak siten, että differentiaaliyhtälö toteutuu.
Koska potenssisarja voidaan suppenemisalueessaan derivoida termeittäin, saadaan derivaattojen lausekkeiksi
| y' | =  kak(x - x0)k-1, kak(x - x0)k-1, | ||
| y'' | = 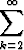 k(k - 1)ak(x - x0)k-2 k(k - 1)ak(x - x0)k-2 | ||
Differentiaaliyhtälön muodosta riippuu, miten helppoa tästä on edetä. Jotta sarjamuotoisen ratkaisun etsiminen ylipäätään olisi mielekästä, on yhtälössä esiinnyttävä vain muuttujan x ja funktion y tai sen derivaattojen polynomeja. Vaatimus yhtälön toteutumisesta tarkoittaa tällöin, että yhtälön eri puolilla esiintyvien muuttujan x samaeksponenttisten potenssien kertoimien pitää olla samat. Tämä johtaa kertoimia ak koskevaan rekursiiviseen yhtälöryhmään, josta ainakin alkupään kertoimet voidaan ratkaista. Usein on myös mahdollista johtaa kertoimille rekursiokaava, jossa seuraava kerroin lausutaan edellisten avulla.
Tuloksena saadaan laskukaavat, joilla potenssisarjan kertoimia voidaan laskea mielivaltaisen pitkälle. Yleisen lausekkeen — kerroin ak indeksin k funktiona — saaminen ei sen sijaan ole aina mahdollista.
Tarkempi kuvaus ratkaisumenetelmän soveltamisesta löytyy esimerkeistä.
Potenssisarjojen teorian mukaan sarja suppenee jollakin muotoa ]x0 - R, x0 + R[ olevalla välillä. Välin keskipisteenä on siis sarjan kehityskeskus x0. Välin päätepisteet voivat tilanteesta riippuen joko kuulua tai olla kuulumatta suppenemisalueeseen. Lukua R sanotaan sarjan suppenemissäteeksi.
Edellä kuvattu ratkaisumenettely ei sellaisenaan anna mitään tietoa saadun sarjan suppenemissäteestä, vaan se on tutkittava erikseen sarjateorian tarjoamilla keinoilla.