Separoituvaan palautuvat ensimmäisen kertaluvun yhtälöt

Vaikka ensimmäisen kertaluvun differentiaaliyhtälö ei olisikaan separoituva, se on toisinaan mahdollista palauttaa separoituvaksi sopivalla sijoituksella.

1) Esimerkiksi jos yhtälö on muotoa

y' = f ,

ts. oikea puoli riippuu vain osamäärästä y/x, mutta ei muulla tavoin muuttujista x ja y, voidaan ottaa käyttöön uusi tuntematon funktio u(x) = y(x)/x eli y(x) = xu(x), jolloin y' = u + xu' . Kun tämä sijoitetaan yhtälöön, se saa muodon

xu' = f(u) - u  eli 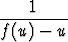  u' = .

Tämä on separoituva.

2) Toinen yksinkertainen esimerkki on muotoa

y' = f(ax + by + c)

oleva yhtälö, missä b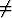0. Valitsemalla uudeksi tuntemattomaksi funktioksi u(x) = ax + by(x) + c saadaan y = (u - ax - c)/b ja y' = (u' - a)/b. Tällöin yhtälö saa muodon

u' = a + bf(u),

mikä on separoituva.