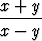 eli y' =
eli y' = 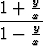
Differentiaaliyhtälössä
y' = 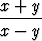 eli y' =
eli y' = 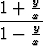
oikea puoli on funktio osamäärästä y/x, jolloin se on muunnettavissa separoituvaksi sijoituksella y(x) = xu(x). Koska tällöin y' = u + xu', saa yhtälö muodon
xu' = 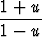 - u eli xu' =
- u eli xu' = 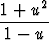 .
.
Separoituna tämä on
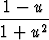 du =
du = 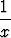 dx
dx
ja puolittainen integrointi antaa
- ln 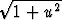 + arctan u = ln|x| + ln|C|.
+ arctan u = ln|x| + ln|C|.
Sijoittamalla u = y/x päädytään yhtälöön
arctan 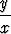 = ln(|C|
= ln(|C|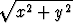 ),
),
mikä siis on differentiaaliyhtälön ratkaisu implisiittisessä muodossa. Kyseessä on transkendenttiyhtälö, josta ei voida ratkaista lauseketta funktiolle y(x), vaikka yhtälö sopivasti rajoitetuilla väleillä funktion määritteleekin.
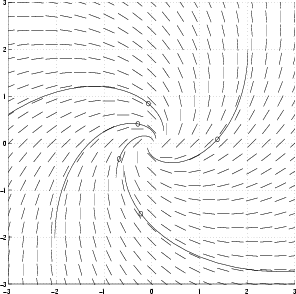
Yhtälön ratkaisukäyriä voidaan tutkia siirtymällä napakoordinaatteihin, so. sijoittamalla
yhtälöön r = 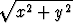 ,
, 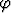 = arctan
= arctan 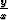 :
:
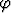 = ln(|C|r) eli r = C1e
= ln(|C|r) eli r = C1e , missä C1 = 1/|C| > 0.
, missä C1 = 1/|C| > 0.
Kyseessä ovat positiiviseen suuntaan auki kiertyvät spiraalit. Sopivasti katkaistut spiraalinkaaret ovat yhtälön ratkaisufunktioiden kuvaajia: