Planeetan liike kiinteän Auringon ympäri

Planeetan liike Auringon ympäri voidaan yksinkertaisimmassa muodossa mallintaa pitämällä Aurinkoa kiinteänä ja ajattelemalla ainoaksi vaikuttavaksi voimaksi Auringon ja planeetan välinen gravitaatio. Todellisuudessa aivan näin ei ole: Planeetta ja Aurinko muodostavat kappaleparin, jossa molemmat vaikuttavat toisiinsa ja kumpikin liikkuu systeemin yhteisen massakeskipisteen suhteen. Liikkuvia kappaleita on myös useampia, Auringon lisäksi monia planeettoja, ja kaikki vaikuttavat toisiinsa. Yksinkertainen malli on suhteellisen hyvä approksimaatio, jos voidaan ajatella, että Auringon massa on merkittävästi planeetan massaa suurempi ja muut planeetat ovat niin etäällä, että niiden vaikutus voidaan jättää huomiotta.

Gravitaatiolain mukaan Auringon ja planeetan välinen vetovoima on

,

missä on Auringon massa ja planeetan massa, 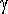on gravitaatiovakio ja r on kappaleiden välinen etäisyys. Oletetaan, että Aurinko sijaitsee origossa ja planeetan paikkavektori on . Tällöin planeettaan kohdistuva voima suuntautuu origoon. Newtonin lain mukaiseksi vektorimuotoiseksi liikeyhtälöksi saadaan

Sievennettynä tämä on

missä . Kyseessä on toisen kertaluvun vektorimuotoinen yhtälö.

Jos oletetaan, että planeetan rata sijaitsee tasossa (mikä ei ole itsestään selvää, mutta seuraa kyllä liikeyhtälöstä), voidaan tason koordinaatteja merkitä x ja y , jolloin paikkavektori on . Differentiaaliyhtälö hajoaa tällöin kahdeksi komponenttiyhtälöksi

Merkitsemällä x ' = u ja y ' = v voidaan tämä palauttaa ensimmäistä kertalukua olevaksi neljän yhtälön normaaliryhmäksi, joka seuraavassa syötetään laskentaa varten Maple en.

Aluksi kuitenkin on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat:

> restart;

Normaaliryhmä on

> ryhma:= diff(x(t), t)=u(t), diff(y(t), t)=v(t), diff(u(t), t)=-alpha*x(t)/(x(t)^2+y(t)^2)^(3/2), diff(v(t), t)=-alpha*y(t)/(x(t)^2 + y(t)^2)^(3/2);

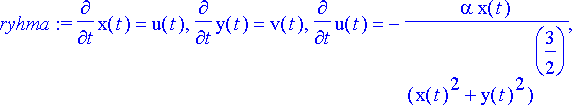
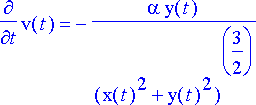
ja probleeman tuntemattomat funktiot

> tuntemattomat:= x(t), y(t), u(t), v(t);

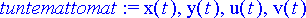
Vakio 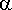on Auringon massan ja gravitaatiovakion tulo (yksikkönä ):

> alpha:= (1.989*10^30)*(6.673*10^(-11));

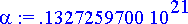
Alkuehdot voidaan antaa vaikkapa jonkin planeetan mukaisesti. Maan keskietäisyys Auringosta on noin 150 miljoonaa kilometriä ja ratanopeus keskimäärin noin 30 kilometriä sekunnissa. Seuraavat alkuehdot ovat tämän mukaisia. Yksikköinä on käytettävä metrejä ja sekunteja kuten eo. vakiossakin:

> alkuehto:= x(0)=0, y(0)=150*10^9, u(0)=30*10^3, v(0)=0;

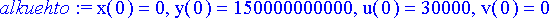
Luontevaa on laskea rata yhden Maan vuoden ajalta yksikkönä sekunti:

> tmax:= 365*24*60*60;

Differentiaaliyhtälöryhmän ratkaisu numeerisesti:

> rtk:= dsolve({ryhma, alkuehto}, {tuntemattomat}, type=numeric, output=listprocedure);

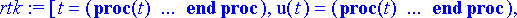
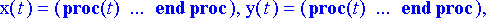
Poimitaan ratkaisusta planeetan paikkaa ilmaisevat komponentit listaksi.

> rata:= subs(rtk, [x(t), y(t)]):

Planeetan rata voidaan piirtää parametrikäyränä; Aurinko sijaitsee origossa.

> plot([rata[1], rata[2], 0..tmax], scaling=constrained);

Ratanopeuden vaihtelusta voidaan myös piirtää kuvaaja:

> ratanopeus:= subs(rtk, sqrt(u(t)^2+v(t)^2));

> plot(ratanopeus, 0..tmax, view=[0..tmax, 0..30000]);

Tehtävä

Tutki, miten alkuehdossa annettu nopeus vaikuttaa rataan. Miten käy, jos nopeutta a) pienennetään, b) suurennetaan, c) sen suuntaa muutetaan? Mitä tapahtuu, jos nopeuden molemmat komponentit ovat = 0? Taivaankappaleiden radat tässä yksinkertaisessa mallissa voivat olla ellipsejä (erikoistapauksena ympyröitä), paraabeleja ja hyperbelejä. Saatko alkuehtoja muuttamalla esiin eri ratatyypit?