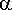Peto- ja saaliskanta

Peto- ja saaliskantojen keskinäistä vuorovaikutusta voidaan mallintaa toisistaan riippuvien differentiaaliyhtälöiden avulla. Tässä tarkastellaan yksinkertaista mallia, joka perustuu ns. Volterran – Lotkan yhtälöihin . Yhtälöt konstruoidaan seuraavalla logiikalla. Saaliseläinkantaa kuvaavan funktion s ( t ) muutokset (derivaatan arvot) riippuvat kahdesta tekijästä. Toisaalta kantaan vaikuttaa ympäristötekijöiden muodostama kasvutermi 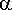s ( t ), joka kuvaa populaation (eksponentiaalista) kasvua olosuhteissa, jossa petokannan vaikutusta ei ole. Tämän lisäksi kantaan vaikuttaa petokannan p ( t ) aiheuttama kantaa vähentävä tekijä. Perusyhtälö saaliskannalle on siis

,

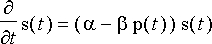jossa 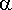on saalispopulaation kasvukerroin ja 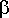on petopopulaationsyömiskerroin. Vastaavasti petokannan yhtälössä tulee olla saaliskannan puuttumisesta aiheutuva kantaa heikentävä (eksponentiaalinen) vähenemistekijä 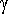p ( t ) sekä saaliskannan runsaudesta aiheutuva kasvutekijä. Niinpä perusyhtälö petokannalle on muotoa

,

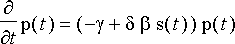missä 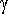on saalistajien vähenemistekijä ja 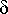on saalistajien tehokerroin saaliseläinten ollessa saatavilla.

Tarkastellaan seuraavaksi, millaisen mallin kantojen käyttäytymiselle yllä esitetyt mallit antavat. Olkoot tarkasteltavina lajeina ilves- ja lumikenkäjäniskannat Kanadassa.

Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.

> restart;

Määritellään ilves- ja jäniskantoja kuvaava differentiaaliyhtälöryhmä (yksikkönä tuhat yksilöä). ( 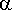= 1.2, 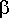= 0.04, 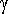= 0.5, 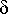= 0.3)

> ryhma:= diff(s(t), t)=s(t)*(1.2-0.04*p(t)), diff(p(t), t)=p(t)*(-0.5 +0.012*s(t));

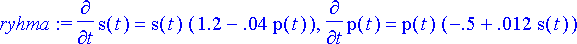
Probleeman tuntemattomat funktiot ovat jäniskantaa kuvaava s ( t ) sekä ilveskantaa kuvaava p ( t ). Aika t kuvaa kuluneita vuosia.

> tuntemattomat:= {s(t), p(t)};

Valitaan kantojen kokoa kuvaavat alkuehdot tarkastelun alkaessa. Ilveksiä olkoon 15 000 ja lumikenkäjäniksiä 60 000 yksilöä.

> alkuehto:= s(0)=60, p(0)=15;

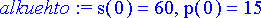
Ratkaistaan differentiaaliyhtälöryhmä.

> rtk:= dsolve({ryhma,alkuehto}, tuntemattomat, type=numeric, output=listprocedure);

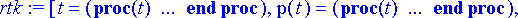
Poimitaan ratkaisusta kantojen koot.

> maarat:= subs(rtk, [s(t), p(t)]):

Piirretään kuvat saaliseläin- ja petokantojen vaihtelusta ajan suhteen.

> plot([maarat[1], maarat[2]], 0..80);

Saamme tulokseksi erittäin säännöllisesti vaihtelevat populaatiot, jossa jäniskanta on merkitty punaisella ja ilveskanta vihreällä käyrällä.

Todellisuudessa vain harvoin ympäristöolot ovat niin tasaiset, että yllä lasketun kaltaista kantojen vaihtelua esiintyisi. Yleensä sää ja muut kannoista riippumattomat ympäristötekijät vaikuttavat merkittävästi populaatioihin. Verrataan kuitenkin saatua tulosta Kanadan lumikenkäjänis- ja ilveskantoihin vuosina 1855 - 1930 (datan alkuperänä on Hudson's Bay Companyn tilastot).

> janis:= [[1855, 76], [1856, 88], [1859, 19], [1861.5, 26], [1862.5, 10], [1863.5, 155], [1865, 151], [1867, 20], [1868, 5], [1871.5, 11], [1872.5, 69], [1873, 51], [1875, 52], [1876, 100], [1877.5, 73], [1881.5, 7], [1882.5, 9], [1884, 43], [1885, 130], [1887, 133], [1889.5, 19], [1892, 62], [1893, 65], [1895, 86], [1897.5, 11], [1899.5, 6], [1901, 12], [1902, 4], [1904, 67], [1906.5, 24], [1907.5, 23], [1909, 24], [1910, 50], [1912.5, 72], [1916.5, 3], [1919, 9], [1921, 57], [1923, 77], [1925, 72], [1926, 10], [1928, 4], [1930, 7]]:

> ilves:= [[1855, 29], [1857, 28], [1861, 4], [1862.5, 4], [1866, 68], [1867.5, 72], [1869, 12], [1872, 7], [1873, 33], [1875, 35], [1876, 48], [1879, 44], [1881, 11], [1882, 11], [1884.5, 50], [1885.5, 78], [1887, 80], [1889, 39], [1892, 21], [1893, 46], [1895, 52], [1901, 9], [1903, 20], [1905.5, 62], [1907, 55], [1908, 5], [1911, 14], [1912, 36], [1915, 43], [1917.5, 6], [1920, 6], [1925, 45], [1927, 52], [1930, 19]]:

> plot([janis, ilves], legend=["Jänis", "Ilves"]);

Havaitaan, että vaikka luonnollisia kannanvaihteluja aiheuttavat myös muut tekijät, on yhdeksän vuoden välein esiintyvä maksimi molemmille kannoille varsin säännöllinen. Volterran–Lotkan yhtälö näyttää siis kuvaavan jotain olennaista saalis-peto-suhteessa olevien kantojen keskinäisestä vuorovaikutuksesta . Toisaalta se ei kerro kovinkaan monesta kannan suuruuteen vaikuttavasta tekijästä.

Tarkastellaan vielä peto- ja saaliskantojen käyttäytymistä faasitasossa. Tarkoituksena on piirtää faasitasokuva, jossa x-akseli kuvastaa kannan kasvunopeutta ja y-akseli kannan suuruutta. Periaatteessa kannan kasvunopeus on kannan kokoa kuvaavan funktion derivaatta. Koska ratkaisu kuitenkin laskettiin numeerisesti, se ei ole funktio jota voitaisiin derivoida. Karkea kuva on sen sijaan mahdollista piirtää laskemalla erotusosamäärän avulla derivaatta tietyissä pisteissä, joiden kautta lopuksi piirretän käyrä.

Lasketaan jäniskannan koko 100 pisteessä:

> spisteet:= seq(maarat[1](t/10), t=0..100):

Lasketaan erotusosamäärän avulla derivaatalle arvio samoissa pisteissä:

> sderivpisteet:= seq((maarat[1](t/10+0.00001)-maarat[1](t/10))/0.00001, t=0..100):

Tehdään vastaavat operaatiot ilveskannalle:

> ppisteet:= seq(maarat[2](t/10), t=0..100):

> pderivpisteet:= seq((maarat[2](t/10+0.00001)-maarat[2](t/10))/0.00001, t=0..100):

Piirretään kantoja kuvaavat kuvaajat samaan kuvaan siten, että x-akselilla on kasvunopeus ja y-akselilla on kannan koko:

> plot([zip((x, y)->[x, y], [sderivpisteet], [spisteet]), zip((x, y)->[x, y], [pderivpisteet], [ppisteet])]);

Tehtäviä

Mitä tämä faasitason kuvaaja kertoo kantojen käyttäytymisestä? Tarkastele, miten eri parametrien muuttaminen vaikuttaa faasitason kuvaajaan.

Tutki myös, onko olemassa alkuehtoja, joiden avulla saavutetaan tasapaino peto- ja saaliskannan välillä. Vihje: Tarkastele alkuehtoa, jossa x '( t ) = y '( t ) = 0.