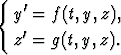
Differentiaaliyhtälöryhmä muodostuu useasta differentiaaliyhtälöstä, joissa tuntemattomia funktioita on yhtä monta kuin yhtälöitä. Voidaan olettaa, että tuntemattomista funktioista ei esiinny muita kuin ensimmäisen kertaluvun derivaattoja. Korkeammat derivaatat voidaan nimittäin poistaa ottamalla käyttöön uusia tuntemattomia funktioita samaan tapaan kuin yhden yhtälön normaaliryhmää muodostettaessa.
Yleensä ryhmä esitetään normaalimuodossa, so. derivaattojen suhteen ratkaistuna. Tällöin esimerkiksi kahden yhtälön ryhmä on muotoa
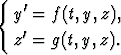
Tuntemattomat funktiot ovat x(t) ja y(t), riippumaton muuttuja t.
Ryhmä, jossa yhtälöitä on n kappaletta ja tuntemattomat funktiot ovat xk(t), k = 1, 2, . . . , n, on vastaavasti
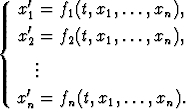
Korkeamman kertaluvun differentiaaliyhtälöä vastaava normaaliryhmä on erikoistapaus tällaisesta normaalimuotoisesta differentiaaliyhtälöryhmästä.
Sovellusten kannalta tärkeimpiä ovat lineaariset differentiaaliyhtälöryhmät. Nämä ovat muotoa
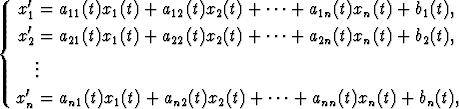
missä funktiot aij(t) ja bi(t) ovat tunnettuja. Jos funktiot aij(t) ovat vakioita, ryhmää sanotaan vakiokertoimiseksi. Jos funktiot bi(t) ovat nollafunktioita, ryhmää sanotaan homogeeniseksi. (Vrt. lineaarista differentiaaliyhtälöä koskeviin nimityksiin.)