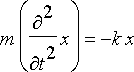Värähtelevä jousi

Jousen puristumista ja venymistä voidaan kuvata varsin yksinkertaisella matemaattisella mallilla. Kun jousi poikkeutetaan tasapainoasemastaan, se pyrkii palautumaan tasapainoasemaan jousivoiman vaikutuksesta. Tälle ns. harmoniselle voimalle pätee

F ( x ) = - kx ,

missä x on jousen poikkeama tasapainoasemasta ja k jouselle tyypillinen jousivakio. Jos toisaalta huomioidaan voima jousisysteemiin aiheuttava kiihtyvyys, saadaan Newtonin lain avulla

F( x ) = ,

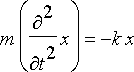missä m on jouseen kiinnitetty massa. Näin on saatu jousen differentiaaliyhtälö.

Yhtälö pätee myös esimerkiksi katosta jousen varassa ripustetulle kappaleelle. Tulee kuitenkin huomata, että kyseinen malli pätee vain pienille poikkeamille x eikä se lainkaan mallinna poikittaista liikettä tai jousessa syntyvää kiertymää.

Otetaan tarkastelun kohteeksi oheisen kuvion mukainen systeemi, jossa kappale massaltaan m on liitetty kattoon jousella, jonka jousivakio on k . Jousi voi liikkua vain pystysuorassa sunnassa.

Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.

> restart;

Kappaleen pystysuora paikkakoordinaatti x ilmoitetaan poikkeamana lepotilasta, ylöspäin positiivisena ja alaspäin negatiivisena. Systeemin liikeyhtälö on Newtonin lain mukainen toisen kertaluvun differentiaaliyhtälö:

> yht:= m*diff(x(t), t$2)+k*x(t)=0;

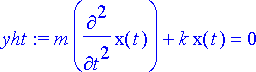
Systeemiä tarkastellaan siten, että kappale sysätään hetkellä t = 0 liikkeelle lepotilasta antamalla sille alkunopeus.

> alkuehdot:= x(0)=0, D(x)(0)=10;

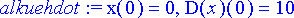
Saatu differentiaaliyhtälö ratkaistaan Maple n dsolve -komennolla.

> rtk:= dsolve({yht, alkuehdot}, x(t));

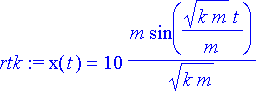
Massa joutuu sinimuotoiseen värähtelyliikkeeseen. Piirretään kuvaaja sijoittamalla ensin arvot massalle ja jousivakiolle.

> rata1:=subs({k=1, m=1}, rtk);

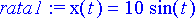
> plot(rhs(rata1), t=0..4*Pi);

Tehdään animaatio värähtelylle. Seuraava koodi määrittelee kappaleen liikkeen animoinnissa tarvittavat työkalut. Kysessä on Maple lla kirjoitettu ohjelmakoodi.

> with(plots): with(plottools):

Warning, the name changecoords has been redefined

> jousi:= proc(ala, yla, paa, jaksot)
local ampl, jakso;
ampl:= 3;
jakso:= (yla-ala-2*paa)/jaksot;
plot(
[[ampl*sin(2*Pi*r/jakso),
r+ala+paa, r=0..jaksot*jakso],
[0, ala+r, r=0..paa],
[0, yla-r, r=0..paa]], color=black);
end:

kappale:= proc(hor, lev, kor)
rectangle([-0.5*lev, hor+0.5*kor],
[0.5*lev, hor-0.5*kor], color=gray)
end:

varahtelija:= proc(y0, t0)
local lev, kor, paa, lepo, y1;
lev:= 20; kor:= 10; paa:= 5; lepo:= 50;
y1:= -lepo+subs(t=t0/(2*Pi), subs(y0,x(t)));
display(
rectangle([-50, 0], [50, 5], color=gray),
kappale(y1, lev, kor),
jousi(y1+kor/2, 0, 5, 5));
end:

Animaatio on lista peräkkäisiä kuvia, jotka on ensin laskettava. Animaatio käynnistyy viemällä hiiren osoitin kuvan päälle ja valitsemalla hiiren oikealla napilla esiin tulevasta valikosta A n imation -> P l ay . Animaatiosta saa jatkuvan valitsemalla em. valikosta A n imation -> C ontinuous .

> display(seq(varahtelija(rata1, u), u=0..39), insequence=true, axes=none, scaling=constrained);

Tehtävä

Tarkastele erisuuruisten massojen käyttäytymistä jousen varassa. Millä tavalla massan muuttaminen vaikuttaa syntyvään värähtelyyn? Entä jos muutamme myös alussa annettua nopeutta siten, että värähtelyn energia pysyy vakiona?