Van der Polin yhtälö

RLC-virtapiirissä oleva vastus vaikuttaa varsin olennaisesti piirissä esiintyviin värähtelyilmiöihin. Kuitenkin aivan uuden elementin komponenttitekniikkaan toivat aikoinaan puolijohdediodeja edeltäneet tyhjiöputket . Tyhjiöputken toiminta perustuu siihen, että putken katodia hehkutetaan ohjausjännitteellä, joka saa sen elektronit karkaamaan tyhjiöön. Putken yli olevan jännitteen ollessa myötäsuuntaan, eletkronit etenevät anodille ja virta kulkee putken läpi. Korkeilla virran arvoilla rajoitettu kuljettajaelektronijoukko aiheuttaa ohmisen vastuksen putken läpi kulkeville elektroneille; tämä vastus kasvaa virran myötä. Virran ollessa heikko putkessa oleva hehkutusjännite ja sen vapauttamat elektronit helpottavat virran kulkua ja putki toimii negatiivisen vastuksen tavoin. Tämä muodostaa uuden, mielenkiintoisen ilmiön: itseaiheutetut oskillaatiot. Näiden oskillaatioiden kuvaamiseen käytetään van der Polin yhtälöä.

Tilanteen lähtökohta on hyvin samankaltainen kuin RLC-virtapiirin yhtälön muodostamissa. Piirissä syntyvät jännitehäviöt perustuvat induktanssiin, resistanssiin ja kapasitanssiin. Kun yhtälö muodostetaan, nämä tekijät ovat

käämin yli,

tyhjiöputken yli sekä

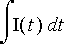kondensaattorin yli.

Ainoa ero syntyy siis tyhjiöputken vastuksesta, joka vakioresistanssin sijaan riippuukin virran suuruudesta yllä esitetyllä tavalla. Virta on vastustermissä merkitty suureettomaksi . Piirretään kuvaaja tyhjiöputken ohmisen vastuksen virtariippuvuudelle.

> plot(i^3/3-i, i=0..3);

Vastus on siis alhaisilla virran arvoilla negatiivinen, ja tyhjiöputken hehkutuksen jännitelähde syöttää energiaa systeemiin. Korkeammilla virran arvoilla vastus muuttuu positiiviseksi.

Piirin yhtälö on

.

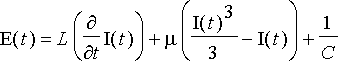
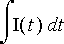Jos piiriin ei syötetä alkuhetken jälkeen ulkoista jännitettä ( E ( t )=0), saadaan virran suhteen derivoimalla homogeeniyhtälö

.

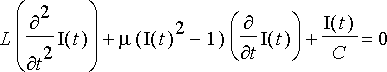Mikäli induktanssi ja kapasitanssi skaalataan ykkösiksi, tämä on perinteinen van der Pol in yhtälö. Ratkaistaan yhtälön virta ajan funktiona.
Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat:

> restart;

Yhtälö normaaliryhmän muotoon kirjoitettuna on

> ryhma:= diff(i(t), t)=v(t), L*diff(v(t), t)+mu*(i(t)^2-1)*v(t)+i(t)/C=0;

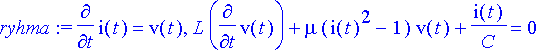
> tuntemattomat:={i(t), v(t)};

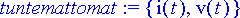
Annetaan vakioille arvot ja muodostetaan alkuehto:

> ryhma1:= subs({L=0.1, C=0.001, mu=0.5}, {ryhma});

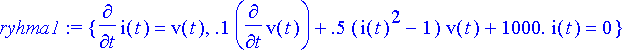
> alkuehto1:= i(0)=0.5, v(0)=0;

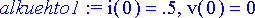
Ratkaistaan yhtälöryhmä.

> rtk:= dsolve({ryhma1[], alkuehto1}, tuntemattomat, type=numeric, output=listprocedure);

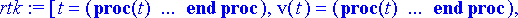
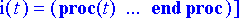
Poimitaan ratkaisusta virtaa ja sen muutosta kuvaava termi.

> virta1:= subs(rtk, [i(t), v(t)]):

Piirretään kuvaaja virralle.

> plot(virta1[1], 0..2, numpoints=200);

Systeemi käyttäytyy van der Pol in yhtälöille tyypillisellä tavalla. Se kehittää virran oskillaatiota, joka kasvaa saturoituen raja-arvoonsa. Huomaa kuitenkin, että alkuvirta tai sen muutos on välttämätön vahvistumisen käynnistämiseksi.

Tarkastellaan systeemiä vielä tilanteessa, jossa alkuvirta on saturaatioarvoa merkittävästi suurempi.

> alkuehto2:= i(0)=5, v(0)=0;

Ratkaistaan yhtälöryhmä.

> rtk2:= dsolve({ryhma1[], alkuehto2}, tuntemattomat, type=numeric, output=listprocedure);

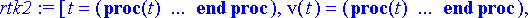
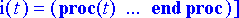
> virta2:= subs(rtk2, [i(t), v(t)]):

Piirretään virralle kuvaaja.

> plot(virta2[1], 0..1);

Esiin tuli van der Pol in yhtälön toinen ominaispiirre. Se rajoittaa erittäin tehokkaasti ylisuuria oskillaatioita ja tuo ne saturaatioarvoonsa. Näin tyhjiöputkipiiri toimii todella tehokkaana värähtelyn tasaajana.

Seuraavaksi tarkastelemme tilannetta faasitasossa, johon piirretään virran ja sen aikaderivaatan saamia arvoja. Tarkastellaan kehitystä matalalla alkuvirralla (vihreä), korkealla alkuvirralla (sininen) sekä tasapainotilanteessa (punainen). Huomaa derivaatan arvon skaalaus tekijällä .

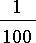> with(plots):

Warning, the name changecoords has been redefined

> display(plot([virta1[1], virta1[2]/100, 0..0.8], color=green), plot([virta2[1], virta2[2]/100, 0..0.35], color=blue), plot([virta1[1], virta1[2]/100, 1.9..2], color=red), scaling=constrained);

Tehtävä

Tämä diagrammi osoittaa hyvin selkeästi van der Polin yhtälön käyttäytymistavan. Faasitason tasapainokäyrä on ympyränmuotoinen sopivalla 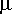:n arvolla, mutta tekijän 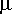suurentaminen johtaa toisenlaisiin värähtelykuvioihin. Kuinka suureksi 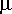tulee määrittää ennen kuin piirin värähtelyssä alkaa esiintyä kulmikkuutta? Miksi piiri käyttäytyy siten?