RCL-vaihtovirtapiiri: vapaa värähtely

Tässä esimerkissä tarkastellaan tavallista RLC-vaihtovirtapiiriä. Piirissä on kolme komponenttia, R ohmin vastus, L henryn induktanssi ja C faradin kapasitanssi.

Piiriin syötettyyn jännitteeseen kohdistuu kolme eri pudotusta,

käämin yli,

vastuksen yli sekä

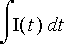kondensaattorin yli.

Näiden summasta syntyy piirin Kirchhoffin lain mukainen sähkömotorinen voima E ( t ). Mikäli piiriin ei syötetä ulkoista jännitettä, on piirin yhtälö

,

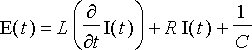
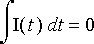Integraalitermistä päästään eroon derivoimalla yhtälö ajan suhteen:

.

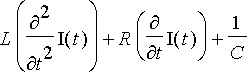
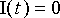Tarkastellaan virran vaimenemista värähtelypiirissä. Oletuksena on tilanne, jossa piiriin on indusoitu hetkellinen virta, mutta tämän jälkeen siihen ei enää syötetä energiaa, ts. virtalähde kytketään pois piiristä. Käsiteltävänä on kaksi eri tapausta, piiri, jossa on ja jossa ei ole vastusta, ts. vaimennettu ja vaimentamaton piiri.

Syötetään piirin yhtälö alkuehtoineen. Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat:

> restart;

Virtaa ja sen muutosnopeutta kuvaava yhtälö.

> yhtalo:= L*diff(i(t), t$2)+R*diff(i(t), t)+i(t)/C=0;

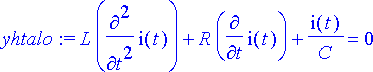
Ongelman tuntematon funktio on virta:

> tuntematon:= i(t);

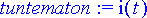
Tarkastellaan tilannetta, missä piirissä jännitelähteen poiskytkentähetkellä kulkeva virta on 100 mA. Annetaan alkuehto.

> alkuehto:= i(0)=0.1, D(i)(0)=0;

Vaimentamaton piiri

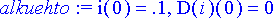
Vaimentamattomassa piirissä on R = 0. Tällöin piirissä oleva sähköinen energia ei kulu vastuksessa lämmöksi. Muut vakiot olkoot L = 0.1 H, C = 1 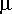F. Yhtälö saa tällöin muodon

> yhtalo1:= subs({L=0.1, R=0, C=0.001}, yhtalo);

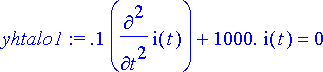
Ratkaistaan differentiaaliyhtälö:

> rtk1:= dsolve({yhtalo1, alkuehto}, tuntematon);

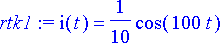
Muokataan ratkaisu käyttökelpoisempaan muotoon.

> virta1:= subs(rtk1, i(t));

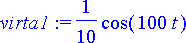
Piiriin syntyy säännöllinen kosinimuotoinen värähtely ilman vaimenemista. Piirretään kuvaaja:

> plot(virta1, t=0..0.3);

Vaimennettu piiri

Kun piiriin lisätään pieni 5 vastus, sen käytös muuttuu olennaisesti.

> yhtalo2:= subs({L=0.1, R=3, C=0.001}, yhtalo);

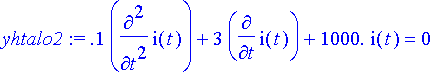
> rtk2:= dsolve({yhtalo2, alkuehto}, tuntematon);

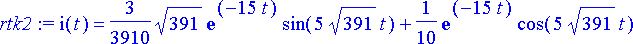
> virta2:= subs(rtk2, i(t)):
simplify(%);

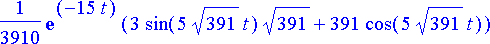
Kyseessä on vaimeneva värähtely, mikä näkyy lausekkeen eksponenttitekijästä. Kuvaaja:

> plot(virta2, t=0..0.3);

Piirissä värähtelevä virta vaimenee vastuksessa häviävän tehon vuoksi. Vaimeneminen on erilaista riippuen vastuksen suuruudesta. Tätä voidaan analysoida seuraavasti: Virtapiirin differentiaaliyhtälö

.

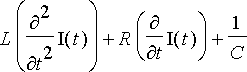
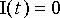on homogeeninen vakiokertoiminen toisen kertaluvun yhtälö. Sen karakteristinen yhtälö on

.

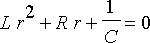Yhtälöllä on joko
1. kaksi imaginaarista juurta ( 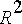< 4 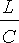), jolloin differentiaaliyhtälö on alivaimennettu kuten esimerkissä;

2. kaksi reaalista juurta ( 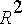> 4 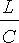), jolloin yhtälö on ylivaimennettu ja virta vaimenee nopeasti nollaksi värähtelemättä, tai
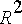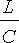3. kaksinkertainen reaalinen juuri ( = 4 ), jolloin yhtälö on kriittisesti vaimentuva eli se vaimenee hitaimmalla mahdollisella tavalla ilman värähtelyä.

Tehtävä

Muunta vastusta säätämällä RLC-vaihtovirtapiirin vaimentumista. Piirrä virtakuvaajat yli-, ja alivaimennetulle sekä kriittisesti vaimennetulle piirille. Tarkastele miten alkuehtojen muuttaminen vaikuttaa kuvaajiin. Voiko kriittisesti vaimennettua piiriä saada värähtelemään sopivalla alkuehtovalinnalla?