| y' = cos x, | y = sin x + C, | ||||||
| y'' + 4y = 0, | y = C1 sin 2x + C2 cos 2x, | ||||||
| y'''(1 + y'2) = 3y'y''2, | (x + C1)2 + (y + C2)2 = C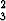 . . |
Differentiaaliyhtälön ratkaisuksi kutsutaan funktiota, joka toteuttaa yhtälön. Esimerkiksi yhtälön y' = cos x ratkaisuna on funktio y(x) = sin x. Tämä ei kuitenkaan ole ainoa ratkaisu, vaan yhtä hyvin ratkaisuksi kelpaa jokainen funktio y(x) = sin x + C, missä C on jokin vakio.
Differentiaaliyhtälön ratkaisu ei yleensä olekaan yksikäsitteinen, vaan ratkaisuja on äärettömän paljon. Tyypillisesti ensimmäisen kertaluvun yhtälön ratkaisut voidaan esittää muodossa, jossa on yksi mielivaltaisesti valittava vakio, toisenkertaluvun yhtälöillä vakioita on kaksi jne.
Tällaista mielivaltaisesti valittavista vakioista riippuvaa ratkaisua kutsutaan differentiaaliyhtälön yleiseksi ratkaisuksi.
Esimerkkeinä eräät yhtälöt ja niiden yleiset ratkaisut:
| y' = cos x, | y = sin x + C, | ||||||
| y'' + 4y = 0, | y = C1 sin 2x + C2 cos 2x, | ||||||
| y'''(1 + y'2) = 3y'y''2, | (x + C1)2 + (y + C2)2 = C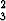 . . |
Antamalla arvot yleisen ratkaisun mielivaltaisille vakioille saadaan differentiaaliyhtälön yksittäisratkaisu.