Lineaarisen ryhmän matriisimuoto

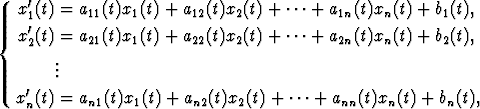
Lineaarinen differentiaaliyhtälöryhmä on muotoa

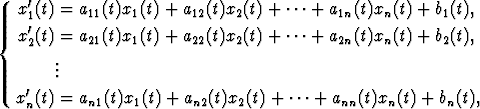
eli

x_j'(t) = 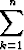a_jk(t)x_k(t) + b_j(t),   j = 1, 2, . . . , n.

Funktiot a_jk (t) ja b_j(t) ovat tunnettuja, funktiot x_j(t) ovat probleeman tuntemattomat.

Muodostamalla kerroinfunktioista ja tuntemattomista funktioista matriisit

A(t) = 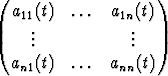,     B(t) = 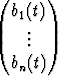,     X(t) =

voidaan yhtälöryhmä kirjoittaa yksinkertaiseen matriisimuotoon

X'(t) = A(t) X(t) + B(t).

Tämä mahdollistaa matriisialgebran ja erityisesti ominaisarvoteorian käytön yhtälöryhmän ratkaisemisessa.

Esimerkiksi jos kyseessä on homogeeninen ryhmä, ts. B(t) = 0, ja kertoimet a_ij(t) ovat vakioita, jolloin A(t) = A on vakiomatriisi, ryhmä saa muodon

X'(t) = A X(t).

Tämän ratkaisu on tapana kirjoittaa muotoon

X(t) = e^tA C,

missä e^tA on eräs neliömatriisi ja C on määräämättömien vakioiden muodostama pystyvektori. Ratkaisu on siten analoginen elementaarin differentiaaliyhtälön y' = ay ratkaisun y = Ce^at kanssa. Edellytyksenä kuitenkin on, että matriisieksponenttifunktio e^tA on ensin määritelty.

Matriisialgebran hyödyntämistä ei tässä lähemmin käsitellä.