10 Viivaintegraali

10.1 Määrittely ja laskeminen

Tehtävä 293

Laske viivaintegraali

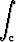(y - x) dx + xy dy,

kun c on a) pisteitä A  (1, 0), B  (-1, 0) yhdistävä x-akselin yläpuolinen yksikköympyrän kaari, b) murtoviiva AP QB, missä P   (1, 1), Q  (-1, 1).

---

Tehtävä 294

Laske viivaintegraali

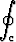(y - x) dx + xy dy,

kun c on positiiviseen suuntaan kierrettynä a) ympyrä x² + y² = 1, b) sen neliön piiri, jonka kärjet ovat (0, 0), (1, 0), (1, 1) ja (0, 1), c) käyrä, jonka muodostavat pisteitä (0, 0) ja (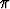, 0) yhdistävät jana ja kaari y = sin x.

Vastaus

---

Tehtävä 295

Laske viivaintegraali

9x²y dx - 11xy² dy,

kun c on origon pisteeseen (1, 1) yhdistävä a) kaari r(t) = t²i + t³j, b) jana, c) kaari r(t) = ti + t^r j, missä vakio r on > 0.

Vastaus

---

Tehtävä 296

Laske viivaintegraali

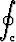(sin y + x⁴y)dx + (xy⁴ + x cos y + x)dy,

missä c on tason yksikköympyrä positiiviseen suuntaan kierrettynä.

Vastaus

---

Tehtävä 297

Laske tason viivaintegraali

,

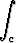
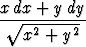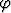
kun c on logaritminen spiraali r = e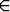^-, [0, 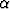]. Onko integraalilla raja-arvoa, kun ?

Vastaus

---

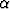
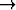
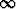Tehtävä 298

Laske viivaintegraali

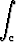yz² dx + xz² dy + 2xyz dz,

kun c on pisteen (0, 0, 0) pisteeseen (1, 2, 3) yhdistävä a) jana, b) kaari r(t) = t i + 2t⁴ j + 3t⁵ k.

Vastaus

---

Tehtävä 299

Laske viivaintegraali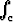 yz² dx + zx² dy + xy² dz, kun c on origon pisteeseen (1, 2, 3) yhdistävä a) jana, b) kaari r(t) = t³ i + 2t⁴ j + 3t⁵ k.

---

Tehtävä 300

Laske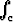 u ^. dr, kun u(x, y, z) = 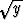i + 2x j + 3y k ja c on käyrän r(t) = t i + t² j + t³ k pisteestä (0, 0, 0) pisteeseen (3, 9, 27) suuntautuva kaari.

Vastaus

---

Tehtävä 301

Olkoon u(x, y, z) = x³i + y²j + zk. Laske

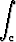u ^. dr,

missä c on origosta pisteeseen (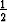, , 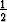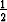) pitkin tason y = z ja pyörähdysparaboloidin z = x² + y² leikkauskäyrää suuntautuva tie.

Vastaus

---

Tehtävä 302

Olkoon u(x, y) = (x² + y²)i - 2xyj ja olkoon c tason yksikköympyrä. Laske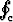 u ^.   dn. (Tässä on dn = n ds, missä n on käyrän c yksikköulkonormaali.)

Vastaus

---

Tehtävä 303

Laske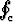 u ^. dn, kun u(x, y) = (x + e^y) i + (sin x + 2y) j ja c on ellipsi x² /a² + y² /b² = 1. (dn = n ds, missä n on käyrän c yksikköulkonormaali.)

---

Tehtävä 304

Olkoon u(x, y, z) = xyzi + y²k. Laske

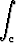u × dr,

missä c on origosta pisteeseen (2, 2, 4) pitkin tason x = y ja parabolisen lieriön z = x² leikkauskäyrää suuntautuva tie.

Vastaus

---

Tehtävä 305

Olkoon

g(u, v) = y dx + 2x dy,

missä c on jana, jonka alkupiste on (0, 0) ja loppupiste (u, v). Määritä funktion g suurin arvo ympyrällä u² + v² = 1.

Vastaus

---

Tehtävä 306

Olkoon M = sup_r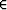c|u(r)| ja L kaaren c pituus. Osoita, että

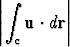< ML.

---

Tehtävä 307

Olkoot c₁ ja c₂ suunnistettuja kaaria, joilla on yhteinen alkupiste ja yhteinen loppupiste. Olkoon c = c₁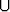 (-c₂). Todista:

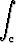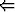
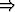
u ^. dr = 0 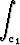u ^. dr = u ^. dr.

---

10.2 Sovellutuksia

Tehtävä 308

Homogeeninen rautalanka taivutetaan puoliympyrän kaaren muotoiseksi. Laske keskiö.

Vastaus

---

Tehtävä 309

Laske keskiö a) asteroidin ensimmäisessä neljänneksessä sijaitsevalle kaarelle r(t) = a cos ³ t i + a sin ³t j, t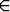 [0, 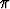/2], b) sykloidin kaarelle r(t) = a(t - sin t)i + a(1 - cos t)j, t 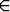[0, 2].

Vastaus

---

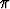Tehtävä 310

Tason paraabelin kaarelle x² = 2y, x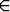 [0, 1], on levitetty massa, jonka tiheys (massa pituusyksikköä kohden) on 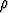(x, y) = x/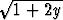. Laske kaaren massakeskipiste. Sijaitseeko tämä kaarella?

Vastaus

---

Tehtävä 311

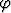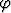
Kirjoita kaavat napakoordinaatistossa annetun sileän kaaren r = r(), 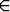[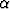, 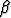], keskiön x- ja y-koordinaateille.

Vastaus

---

Tehtävä 312

Todista Guldinin toinen sääntö: Jos tasokäyrän kaari pyörähtää samassa tasossa olevan akselin ympäri, joka ei leikkaa kaarta, niin syntyvän pyörähdyspinnan ala on kaaren pituus kerrottuna kaaren keskiön kulkemalla matkalla.

---

Tehtävä 313

Ympyrä, jonka säde on R, pyörähtää samassa tasossa olevan akselin ympäri, jonka etäisyys ympyrän keskipisteestä on L. Olkoon L > R. Laske Guldinin säännön avulla syntyvän kappaleen (toruksen) pinta-ala.

Vastaus

---

10.3 Riippumattomuus tiestä

Tehtävä 314

Laske viivaintegraali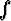 r ^. dr, kun integroimistien alkupisteenä on origo ja loppupisteenä P₀  r₀. Totea, että integraali ei riipu integroimistiestä. Mikä on vektorikentän u(r) = r potentiaali?

Vastaus

---

Tehtävä 315

Osoita, että viivaintegraali

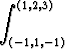yz dx + zx dy + xy dz

on alku- ja loppupistettä yhdistävästä tiestä riippumaton ja laske integraali. Voidaanko integraali kirjoittaa muotoon 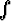g ^. dr, kun funktio g valitaan sopivasti?

Vastaus

---