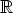 upotetaan kompleksitasoon
upotetaan kompleksitasoon 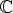 samastamalla
samastamalla 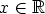 ja
ja
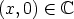 . Tällöin aletaan myös merkitä
. Tällöin aletaan myös merkitä 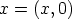 . Kompleksitason
nollalle ja ykköselle saadaan tällöin luonnolliset merkinnät:
. Kompleksitason
nollalle ja ykköselle saadaan tällöin luonnolliset merkinnät: 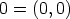 ja
ja
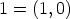 .
.
Reaalilukujoukko 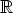 upotetaan kompleksitasoon
upotetaan kompleksitasoon 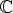 samastamalla
samastamalla 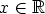 ja
ja
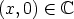 . Tällöin aletaan myös merkitä
. Tällöin aletaan myös merkitä 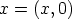 . Kompleksitason
nollalle ja ykköselle saadaan tällöin luonnolliset merkinnät:
. Kompleksitason
nollalle ja ykköselle saadaan tällöin luonnolliset merkinnät: 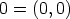 ja
ja
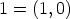 .
.
Samastus johtaa merkintään, jota yleensä käytetään kompleksilukuja käsiteltäessä:
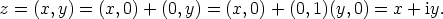
Tässä 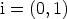 on imaginaariyksikkö.
on imaginaariyksikkö.
Kompleksiluvun 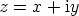 reaaliosa on
reaaliosa on 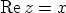 ja imaginaariosa
ja imaginaariosa 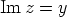 .
Lukua
.
Lukua 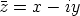 kutsutaan luvun
kutsutaan luvun  liittoluvuksi eli konjugaatiksi.
liittoluvuksi eli konjugaatiksi.
Kompleksiluvun 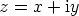 itseisarvo on
itseisarvo on 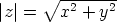 , ts. pisteen
, ts. pisteen 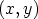 etäisyys origosta. On myös voimassa
etäisyys origosta. On myös voimassa 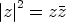 (mutta
(mutta 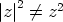 , jos
, jos  on
aidosti kompleksinen, ts.
on
aidosti kompleksinen, ts. 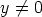 ).
).
Reaalilukujen samastaminen kompleksilukujen osajoukoksi ei ole järkevää, elleivät kummassakin joukossa toisistaan riippumatta määritellyt laskutoimitukset ole myös samastettavissa. Tämä tarkoittaa, että laskutoimituksen tuloksen täytyy olla riippumaton siitä, kumpi suoritetaan ensin, samastus vai laskutoimitus. Näin todella on, mikä ilmenee seuraavista kommutoivista kaavioista: niissä päästään vasemmasta ylänurkasta oikeaan alanurkkaan kumpaa tahansa tietä.
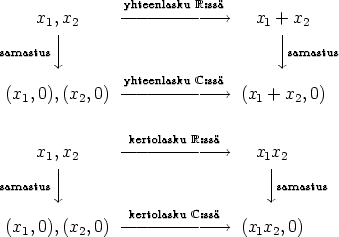
Tuloksena on saatu kompleksilukujoukko 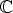 , jonka luvut ovat muotoa
, jonka luvut ovat muotoa 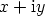 .
Näiden peruslakutoimitukset yhteen-, vähennys- (= vastaluvun lisäys), kerto- ja
jakolasku (= käänteisluvulla kertominen) noudattavat samoja sääntöjä kuin
reaalilukujoukossa. Lisäksi lausekkeita voidaan sieventää yhtälön
.
Näiden peruslakutoimitukset yhteen-, vähennys- (= vastaluvun lisäys), kerto- ja
jakolasku (= käänteisluvulla kertominen) noudattavat samoja sääntöjä kuin
reaalilukujoukossa. Lisäksi lausekkeita voidaan sieventää yhtälön 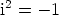 avulla.
avulla.
Linkkejä
Kompleksilukujen määrittely
Kompleksilukujen napakoordinaattiesitys
Simo K. Kivelä 21.04.2005