Napakoordinaattiesitys
Kompleksiluku 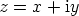 voidaan ajatella xy-tason pisteeksi
voidaan ajatella xy-tason pisteeksi 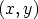 . Itseisarvo
. Itseisarvo
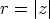 on pisteen etäisyys origosta. Origosta pisteeseen osoittavan janan
suuntakulma x-akseliin nähden (napakulma) olkoon
on pisteen etäisyys origosta. Origosta pisteeseen osoittavan janan
suuntakulma x-akseliin nähden (napakulma) olkoon 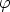 . Tämä on positiivinen
tai negatiivinen sen mukaan, kierretäänkö positiiviseen tai negatiiviseen
kiertosuuntaan. Luontevaa (joskaan ei välttämätöntä) on rajoittaa suuntakulma
väliin
. Tämä on positiivinen
tai negatiivinen sen mukaan, kierretäänkö positiiviseen tai negatiiviseen
kiertosuuntaan. Luontevaa (joskaan ei välttämätöntä) on rajoittaa suuntakulma
väliin 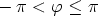 .
.
Tällöin kompleksiluvulle saadaan napakoordinaattiesitys 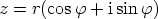 .
.
Suorakulmaisten ja napakoordinaattien väliset yhteydet ovat
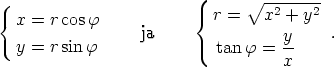
Viimeinen yhtälö voidaan kirjoittaa muotoon 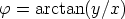 vain, jos
vain, jos 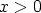 .
Jos
.
Jos 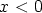 , on saatua arvoa korjattava jaksotermillä
, on saatua arvoa korjattava jaksotermillä 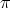 (lisättävä tai
vähennettävä), jotta päästään oikeaan xy-tason neljännekseen.
(lisättävä tai
vähennettävä), jotta päästään oikeaan xy-tason neljännekseen.
Kompleksiluvun itseisarvoa kutsutaan myös moduuliksi ja napakulmaa
argumentiksi; merkinnät 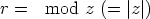 ,
, 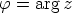 .
.
Linkkejä
Kompleksilukujen suorakulmainen esitys
Kompleksilukujen tulo
Simo K. Kivelä 25.04.2005
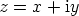 voidaan ajatella xy-tason pisteeksi
voidaan ajatella xy-tason pisteeksi 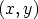 . Itseisarvo
. Itseisarvo
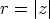 on pisteen etäisyys origosta. Origosta pisteeseen osoittavan janan
suuntakulma x-akseliin nähden (napakulma) olkoon
on pisteen etäisyys origosta. Origosta pisteeseen osoittavan janan
suuntakulma x-akseliin nähden (napakulma) olkoon 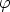 . Tämä on positiivinen
tai negatiivinen sen mukaan, kierretäänkö positiiviseen tai negatiiviseen
kiertosuuntaan. Luontevaa (joskaan ei välttämätöntä) on rajoittaa suuntakulma
väliin
. Tämä on positiivinen
tai negatiivinen sen mukaan, kierretäänkö positiiviseen tai negatiiviseen
kiertosuuntaan. Luontevaa (joskaan ei välttämätöntä) on rajoittaa suuntakulma
väliin 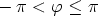 .
.
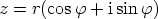 .
.
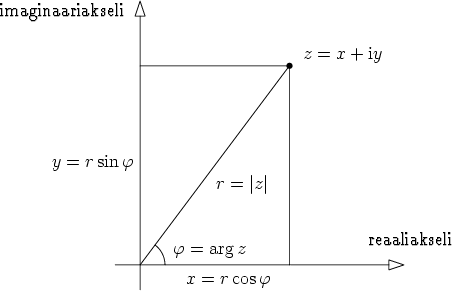
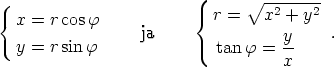
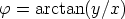 vain, jos
vain, jos 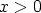 .
Jos
.
Jos 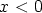 , on saatua arvoa korjattava jaksotermillä
, on saatua arvoa korjattava jaksotermillä 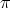 (lisättävä tai
vähennettävä), jotta päästään oikeaan xy-tason neljännekseen.
(lisättävä tai
vähennettävä), jotta päästään oikeaan xy-tason neljännekseen.
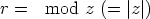 ,
, 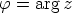 .
.