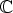 on algebralliselta
struktuuriltaan kunta (kuten reaaliluvutkin). Tämän osoittamiseksi on todettava
seuraavien kunta-aksioomien voimassaolo:
on algebralliselta
struktuuriltaan kunta (kuten reaaliluvutkin). Tämän osoittamiseksi on todettava
seuraavien kunta-aksioomien voimassaolo:
Yhteen- ja kertolaskulla varustettu kompleksilukujen joukko 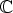 on algebralliselta
struktuuriltaan kunta (kuten reaaliluvutkin). Tämän osoittamiseksi on todettava
seuraavien kunta-aksioomien voimassaolo:
on algebralliselta
struktuuriltaan kunta (kuten reaaliluvutkin). Tämän osoittamiseksi on todettava
seuraavien kunta-aksioomien voimassaolo:
Linkkejä
Kunnan käsite
Kompleksilukujen määrittely
Kunta-aksioomien todistaminen (Mathematica)
Simo K. Kivelä 21.04.2005