
Olkoon annettuna kaksi kompleksilukua napakoordinaattimuodossa:

Lukujen itseisarvot ovat 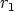 ja
ja 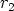 , niiden napakulmat (argumentit)
, niiden napakulmat (argumentit) 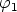 ja
ja
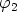 .
.
Lukujen tulo saadaan sinin ja kosinin yhteenlaskukaavojen avulla muotoon
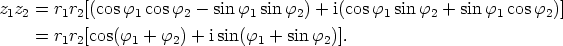
Vastaavaan tapaan saadaan luvun 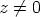 ,
, 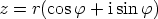 käänteisluvulle
käänteisluvulle
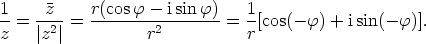
Kummassakin tapauksessa tulokset ovat napakoordinaattimuotoja. Lukujen tulon
itseisarvo on siis 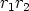 ja napakulma
ja napakulma 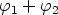 . Käänteisluvun muodostuksessa
itseisarvo muuttuu käänteisluvuksi ja napakulma vastaluvuksi. Siis:
. Käänteisluvun muodostuksessa
itseisarvo muuttuu käänteisluvuksi ja napakulma vastaluvuksi. Siis:
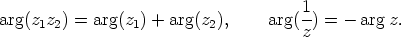
Jos 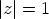 , luku voidaan kirjoittaa muotoon
, luku voidaan kirjoittaa muotoon 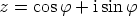 . Edellä
esitetystä seuraa tällöin
. Edellä
esitetystä seuraa tällöin 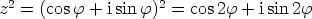 ja yleisemmin
ns. de Moivren kaava
ja yleisemmin
ns. de Moivren kaava
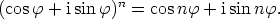
Tässä 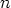 voi olla mikä tahansa kokonaisluku, mikä nähdään yhdistämällä edellä
olevat tuloa ja käänteislukua koskevat tulokset.
voi olla mikä tahansa kokonaisluku, mikä nähdään yhdistämällä edellä
olevat tuloa ja käänteislukua koskevat tulokset.
Linkkejä
Kompleksiluvun napakoordinaattiesitys
Kiertotekijä
Kompleksiluvun juuret
Kompleksilukujen tulo (interaktiivinen dokumentti)
Simo K. Kivelä 26.04.2005