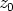 reaalikertoimisen polynomin
reaalikertoimisen polynomin 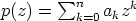 kompleksinen
nollakohta. Tällöin on
kompleksinen
nollakohta. Tällöin on
Olkoon 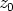 reaalikertoimisen polynomin
reaalikertoimisen polynomin 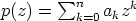 kompleksinen
nollakohta. Tällöin on
kompleksinen
nollakohta. Tällöin on
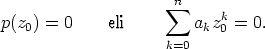
Siirtymällä puolittain liittolukuihin saadaan
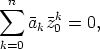
koska summan ja tulon liittoluvut voidaan muodostaa termeitttäin ja tekijöittäin. Polynomin reaalikertoimisuuden takia tämä saa muodon
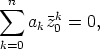
ts. 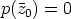 .
.
Siis:
Jos reaalikertoimisella polynomilla on nollakohtana kompleksiluku 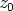 , myös
liittoluku
, myös
liittoluku 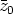 on polynomin nollakohta. Reaalikertoimisen polynomin kompleksiset
juuret esiintyvät aina tällä tavoin pareittain.
on polynomin nollakohta. Reaalikertoimisen polynomin kompleksiset
juuret esiintyvät aina tällä tavoin pareittain.
Tällaisessa tapauksessa polynomin esityksessä ensimmäisen asteen tekijöiden
avulla on tekijät 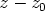 ja
ja 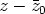 . Näiden tulo on
. Näiden tulo on
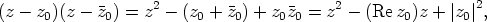
mikä on reaalikertoiminen toisen asteen tekijä.
Siis:
Reaalikertoiminen polynomi voidaan aina jakaa enintään toista astetta oleviin reaalikertoimisiin tekijöihin. Reaalisia nollakohtia vastaavat ensimmäisen asteen tekijät, nollakohtina olevia liittolukupareja vastaavat toisen asteen tekijät.
Linkkejä
Polynomin tekijöihin jako
Esimerkki polynomin tekijöihin jakamisesta
Simo K. Kivelä 03.05.2005