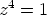 seuraa
seuraa 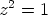 ja
ja 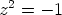 ja näistä edelleen
yhtälön juuret
ja näistä edelleen
yhtälön juuret 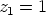 ,
, 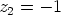 ,
, 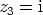 ja
ja 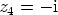 . Polynomin
. Polynomin 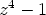 nollakohdat ovat siten
nollakohdat ovat siten 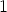 ,
, 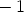 ,
, 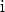 ja
ja 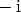 , jolloin se voidaan jakaa ensiasteisiin
tekijöihin seuraavasti:
, jolloin se voidaan jakaa ensiasteisiin
tekijöihin seuraavasti:
Esimerkki 1. Yhtälöstä 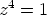 seuraa
seuraa 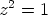 ja
ja 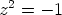 ja näistä edelleen
yhtälön juuret
ja näistä edelleen
yhtälön juuret 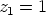 ,
, 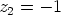 ,
, 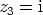 ja
ja 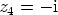 . Polynomin
. Polynomin 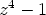 nollakohdat ovat siten
nollakohdat ovat siten 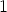 ,
, 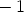 ,
, 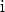 ja
ja 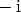 , jolloin se voidaan jakaa ensiasteisiin
tekijöihin seuraavasti:
, jolloin se voidaan jakaa ensiasteisiin
tekijöihin seuraavasti:
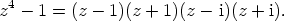
Kahden viimeisen tekijän tulo on reaalikertoiminen toisen asteen polynomi, jolloin päästään reaalikertoimiseen tekijöihin jakoon:
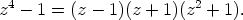
Esimerkki 2. Polynomin 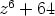 nollakohdat eli juuren
nollakohdat eli juuren 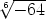 kaikki arvot
ovat
kaikki arvot
ovat
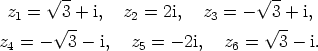 |
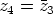 ,
, 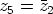 ja
ja 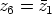 .
.
Polynomin jako ensimmäisen asteen tekijöihin on kompleksikertoiminen:
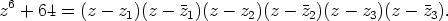
Kun tekijät yhdistetään pareittain, saadaan
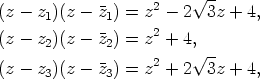
jolloin saadaan jako reaalikertoimisiin toisen asteen tekijöihin:
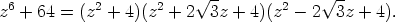
Linkkejä
Polynomin tekijöihin jako
Polynomin jako reaalisiin tekijöihin
Simo K. Kivelä 11.05.2005