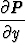 = 1 ja
= 1 ja 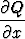 = 2xy - 1
= 2xy - 1
1) Differentiaaliyhtälön y + (x2y - x)y' = 0 kerroinfunktiot ovat P (x, y) = y ja Q(x, y) = x2 y - x. Koska osittaisderivaatat
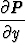 = 1 ja
= 1 ja 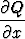 = 2xy - 1
= 2xy - 1
ovat eri suuret, yhtälö ei ole eksakti.
Jos yhtälö kerrotaan tekijällä 1/x2, se saa muodon
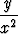 +
+ 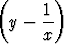 y' = 0.
y' = 0.
Tällöin
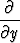
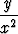 =
= 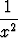 =
= 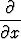
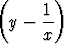 ,
,
ja yhtälö siis on eksakti. Kerroin 1/x2 on yhtälön integroiva tekijä.
Yhtälö voidaan tällöin ratkaista eksaktiuteen perustuen. Tulos on
-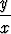 +
+ 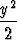 = C eli xy2 - 2y = 2Cx.
= C eli xy2 - 2y = 2Cx.
2) Joissakin erikoistapauksissa voidaan sopiva integroiva tekijä etsiä laskemalla. Esimerkkinä olkoon yhtälö (2xy - y2 - y) + (2xy - x2 - x)y' = 0, jolle yritetään etsiä muotoa M(x + y) oleva integroiva tekijä. Tässä M on siis yhden muuttujan funktio, jonka argumenttina on summa x + y.
Kun yhtälö kerrotaan integroivalla tekijällä saadaan kerroinfunktioiksi
P (x, y) = M(x + y)(2xy - y2 - y), Q(x, y) = M(x + y)(2xy - x2 - x).
Eksaktiusehto 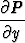 =
= 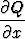 antaa tällöin
antaa tällöin
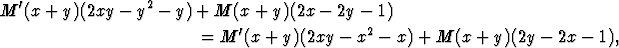 |
M' (x + y)(x + y + 1) = -4M(x + y) eli M'(t)(t + 1) = -4M(t);
tässä on merkitty t = x + y. Saatu yhtälö on separoituva, ja sen eräs ratkaisu on M(t) = 1/(t + 1)4, jolloin integroivaksi tekijäksi saadaan
M(x + y) = 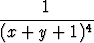 .
.
Tällöin yhtälöstä tulee eksakti ja se voidaan ratkaista. Tulos voidaan kirjoittaa muotoon
xy = C(x + y + 1)3.