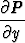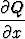Eksakti differentiaaliyhtälö

Käyräparven F (x, y) = C differentiaaliyhtälöä johdettaessa yhtälö derivoidaan muuttujan x suhteen, jolloin saadaan

F_x(x, y) + F_y(x, y)y' = 0,

missä alaindeksit tarkoittavat osittaisderivaattoja. Tämä on parven differentiaaliyhtälö, koska se ei enää sisällä vakiota C.

Kääntäen voidaan kysyä, onko mahdollista ratkaista differentiaaliyhtälö

P (x, y) + Q(x, y)y' = 0

tulkitsemalla P (x, y) ja Q(x, y) jonkin funktion F (x, y) osittaisderivaatoiksi, jolloin ratkaisu olisi F (x, y) = C.

Yleisesti näin ei ole. Jos nimittäin olisi P (x, y) = F_x(x, y) ja Q(x, y) = F_y(x, y), olisi sangen yleisillä edellytyksillä voimassa olevan sekaderivaattojen yhtäsuuruuden takia

P_y(x, y) = F_xy(x, y) = F_yx(x, y) = Q_x(x, y).

Ainakin siis tulee olla voimassa

P_y(x, y) = Q_x(x, y)  eli   = .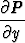

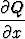Voidaan osoittaa, että tämä ehto on myös riittävä funktion F olemassaololle. Tällöin sanotaan, että differentiaaliyhtälö on eksakti.

Eksakti differentiaaliyhtälö P (x, y) + Q(x, y)y' = 0 voidaan siten ratkaista integroimalla funktio P (x, y) muuttujan x suhteen, jolloin saadaan

F (x, y) = 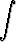P (x, y) dx + f(y).

Tässä integroimisvakio f(y) riippuu muuttujasta y, joka on integroinnin kannalta vakio. Funktio f(y) on määrättävä ehdosta F_y(x, y) = Q(x, y), minkä jälkeen differentiaaliyhtälön ratkaisu saadaan muodossa F (x, y) = C.