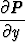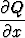= 
.
Differentiaaliyhtälö
P (x, y) + Q(x, y)y' = 0
on eksakti, jos sen kerroinfunktioille pätee
= .
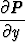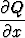Ratkaisu löydetään tällöin muodossa F (x, y) = C. Funktion F (x, y) osittaisderivaatat ovat P (x, y) ja Q(x, y).
Jos yhtälö ei ole eksakti, saattaa olla mahdollista löytää funktio M(x, y) siten, että tällä kerrottu alkuperäinen yhtälö
M(x, y)P (x, y) + M(x, y)Q(x, y)y' = 0
on eksakti, ts.
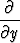[M(x, y)P (x, y)] = 
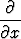[M(x, y)Q(x, y)].
Funktiota M(x, y) kutsutaan tällöin yhtälön integroivaksi tekijäksi.
Ratkaisemisessa voidaan tämän jälkeen edetä kuten eksaktien yhtälöiden ratkaisemisessa.
Yleistä menettelyä integroivan tekijän löytämiseen ei kuitenkaan ole. Eksaktiusehto
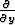(MP ) = 
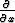(MQ) on nimittäin osittaisdifferentiaaliyhtälö eikä se yleensä ole
alkuperäistä yhtälöä yksinkertaisempi. Joitakin menettelytapaohjeita integroivan
tekijän etsimiseen voidaan erikoistapauksissa esittää, mutta näiden merkitys on
vähäinen.