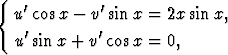
Toisen kertaluvun lineaarinen epähomogeeninen yhtälö: yksittäisratkaisu vakioiden varioinnilla

Toisen kertaluvun lineaarista epähomogeenista yhtälöä

y'' + y = 2x sin x

vastaava homogeeniyhtälö y'' + y = 0 on vakiokertoiminen, ja sen yleinen ratkaisu on y = C₁ sin x + C₂ cos x.

Epähomogeenisen yhtälön yksittäisratkaisun muoto on vaikeasti arvattavissa. Ainoaksi mahdollisuudeksi jää tällöin soveltaa yleistä vakioiden variointi -menettelyä, jolloin yritteeksi otetaan y = u(x) sin x + v(x) cos x ja pyritään määrittämään funktiot u ja v siten, että tämä toteuttaa yhtälön.

Yritteen derivaatta on y' = u cos x - v sin x + u' sin x + v' cos x, mutta tätä yksinkertaistetaan asettamalla lisäehto

u' sin x + v' cos x = 0,

jolloin y' = u cos x - v sin x. Toinen derivaatta on tällöin y'' = -u sin x - v cos x + u' cos x - v' sin x. Derivaattojen sijoittaminen differentiaaliyhtälöön johtaa itse funktioiden u ja v supistumiseen pois (näin käy menettelyssä aina), ja jäljelle jää vain derivaattoja koskeva yhtälö

u' cos x - v' sin x = 2x sin x.

Derivaatoille u' ja v' on tällöin saatu lineaarinen yhtälöryhmä

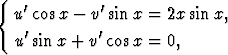
josta ratkaisemalla saadaan

u' = 2x sin x cos x = x sin 2x,   v' = -2x sin ²x = x(cos 2x - 1).

Näiden integrointi antaa

u(x) = 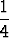sin 2x - 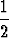x cos 2x + vakio,   v(x) = 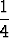cos 2x + 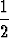x sin 2x - 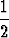x² + vakio.

Etsitty yksittäisratkaisu on tällöin y = u(x) sin x + v(x) cos x. Asettamalla vakiot = 0 ja sieventämällä trigonometrisesti tämä voidaan saada muotoon

y = u(x) sin x + v(x) cos x = 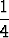cos x + 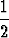x sin x - 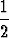x² cos x.

Epähomogeenisen yhtälön yleinen ratkaisu saadaan laskemalla yhteen homogeeniyhtälön yleinen ratkaisu ja saatu yksittäisratkaisu. Koska vakiot C₁ ja C₂ ovat mielivaltaisia, voidaan yksittäisratkaisun termi cos x ajatella yhdistettäväksi termiin C₂ cos x, jolloin yleiseksi ratkaisuksi saadaan

y = C₁ sin x + C₂ cos x + 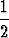(x sin x - x² cos x).