Toisen kertaluvun lineaarinen ja epähomogeeninen yhtälö

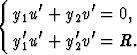
Yleisen teorian mukaan toisen kertaluvun epähomogeenisen yhtälön y'' + P₁(x)y' + P₀(x)y = R(x) yleinen ratkaisu saadaan lisäämällä vastaavan homogeeniyhtälön y'' + P₁(x)y' + P₀(x)y = 0 yleiseen ratkaisuun jokin epähomogeenisen yhtälön yksittäisratkaisu.

Ratkaiseminen tapahtuu siten kahdessa vaiheessa: Ensin on löydettävä vastaavan homogeeniyhtälön ratkaisu y = C₁y₁(x) + C₂y₂(x). Tämän jälkeen haetaan jokin — mikä tahansa — epähomogeeniyhtälön ratkaisu.

Epähomogeeniyhtälön yksittäisratkaisu voidaan toisinaan löytää arvaamalla sen periaatteellinen muoto ja sijoittamalla yhtälöön vastaava yrite.

Myös yleinen menettely on olemassa, mutta se on suhteellisen monimutkainen. Samaan tapaan kuin ensimmäisen kertaluvun tapauksessa sitä kutsutaan vakioiden varioinniksi, koska yritteenä käytetään homogeeniyhtälön yleisestä ratkaisusta saatavaa lauseketta, jossa vakiot C₁ ja C₂ on korvattu tuntemattomilla funktioilla u ja v: yrite on siten y = u(x)y₁ (x) + v(x)y₂(x). Tuntemattomat funktiot pyritään määräämän siten, että tämä toteuttaa yhtälön.

Differentiaaliyhtälöön sijoittamista varten yrite on derivoitava kahdesti. Ensimmäinen derivaatta on y' = u'y₁ + v'y₂ + uy₁' + vy₂', mutta tämän lauseketta yksinkertaistetaan asettamalla funktioille u ja v lisävaatimus u'y₁ + v'y₂ = 0, jolloin y' = uy₁' + vy₂'. Lisävaatimus on periaatteessa mielivaltainen. Koska tavoitteena kuitenkin on löytää vain jotkin funktiot u ja v, tällainen voidaan asettaa, jos osoittautuu, että ratkaisu voidaan lisärajoituksesta huolimatta löytää.

Koska y' = uy₁' + vy₂', on toinen derivaatta y'' = u'y₁' + v'y₂' + uy₁'' + vy₂''. Yritteen sijoittaminen differentiaaliyhtälöön ja termien ryhmittäminen sopivasti antaa tällöin ehdon

u(y₁ '' + P₁y₁' + P₀y₁) + v(y₂'' + P₁y₂' + P₀y₂) + u'y₁' + v'y₂' = R.

Koska y₁ ja y₂ toteuttavat vastaavan homogeeniyhtälön, kaksi ensimmäistä termiä ovat = 0, ja jäljelle jää ehto u'y₁' + v'y₂' = R. Asetetun lisävaatimuksen on myös toteuduttava, jolloin funktioiden u ja v derivaatoille saadaan lineaarinen yhtälöryhmä

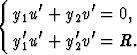
Tästä voidaan ratkaista derivaatat u' ja v', minkä jälkeen integroimalla saadaan funktiot u ja v. Etsitty yksittäisratkaisu y = u(x)y₁(x) + v(x)y₂(x) on siis löydetty.

Ongelmana on kuitenkin, saadaanko derivaatat aina ratkaistuiksi lineaarisesta yhtälöryhmästä. Tällaisellahan ei välttämättä ole ratkaisua. Riittävä ehto ratkaisun olemassaololle on, että ryhmän kerroindeterminantti

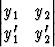
poikkeaa nollasta. Näin tässä tapauksessa onkin (jopa kaikilla tarkasteluväliin kuuluvilla muuttujan x avoilla), koska kyseessä on homogeeniyhtälön perusratkaisujen Wronskin determinantti, joka on 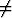0 perusratkaisujen lineaarisen riippumattomuuden takia.