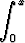
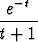 dt.
dt.
Toisen kertaluvun lineaarista epähomogeenista alkuarvoprobleemaa
(x + 1)y'' - xy' - y = (x + 1)2, y(0) = y'(0) = 0
vastaavan homogeeniyhtälön yleinen ratkaisu on
y = C1ex + C2ex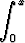
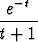 dt.
dt.
Epähomogeenisen yhtälön yleinen ratkaisu saadaan lisäämällä tähän jokin epähomogeenisen yhtälön yksittäisratkaisu.
Yhtälön muodon perusteella saattaisi olla mahdollista löytää yksittäisratkaisuksi toisen asteen polynomi. Sopiva yrite olisi siten y = ax2 + bx + c, missä kertoimet a, b ja c määritetään siten, että yhtälö toteutuu.
Sijoittamalla yrite yhtälöön saadaan
2a(x + 1) - x(2ax + b) - (ax2 + bx + c) = (x + 1)2.
Tämä sievenee muotoon
-3ax2 + 2(a - b)x + (2a - c) = x2 + 2x + 1.
Jotta oikean ja vasemman puolen polynomit olisivat samat, tulee kertoimien olla samat:
-3a = 1, a - b = 1, 2a - c = 1. Tästä seuraa a = -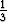 , b = -
, b = -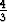 , c = -
, c = -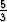 , jolloin
yksittäisratkaisu on
, jolloin
yksittäisratkaisu on
y = -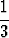 (x2 + 4x + 5).
(x2 + 4x + 5).
Differentiaaliyhtälön yleinen ratkaisu on siis
y = C1ex + C2ex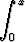
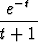 dt -
dt - 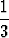 (x2 + 4x + 5).
(x2 + 4x + 5).
Alkuarvoprobleeman ratkaisu saadaan vaatimalla, että yleinen ratkaisu toteuttaa
alkuehdot. Ehdosta y(0) = 0 seuraa C1 - 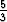 = 0. Koska
= 0. Koska
y' = C1ex + C2ex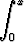
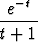 dt +
dt + 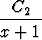 -
- 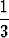 (2x + 4),
(2x + 4),
seuraa ehdosta y'(0) = 0 yhtälö C1 + C2 - 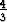 = 0. On siis oltava C1 =
= 0. On siis oltava C1 = 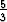 ja C2 = -
ja C2 = -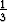 .
Alkuarvoprobleeman ratkaisu on siten
.
Alkuarvoprobleeman ratkaisu on siten
y = 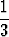
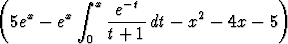 alueessa x > -1.
alueessa x > -1.