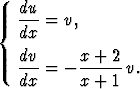
Toisen kertaluvun lineaarisessa ja homogeenisessa differentiaaliyhtälössä
(x + 1)y'' - xy' - y = 0
on kerroinfunktioiden x + 1, -x ja -1 summa = 0, jolloin sillä on ratkaisuna ainakin y = ex .
Yleiseen ratkaisuun tarvitaan kuitenkin kaksi lineaarisesti riippumatonta yksittäisratkaisua. Kun toinen tiedetään, toinen voidaan aina etsiä yritteellä, jossa tunnettu ratkaisu kerrotaan tuntemattomalla funktiolla; tässä tapauksessa y = u(x)ex .
Sijoittamalla yrite yhtälöön saadaan
(x + 1)(u'' + 2u' + u)ex - x(u' + u)ex - uex = 0,
mikä sievenee muotoon
(x + 1)(u'' + 2u') - xu' = 0.
Jäljelle jää siis vain funktion u derivaattoja, funktio itse supistuu pois. Menettelyssä käy aina tällä tavoin.
Saatua yhtälöä vastaava normaaliryhmä on
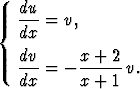
Jälkimmäinen yhtälö on separoituva ja antaa
v = 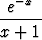 ,
,
jolloin u saadaan yhdellä lisäintegroinnilla:
u = 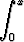
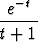 dt.
dt.
Integraali ei ole lausuttavissa alkeisfunktioiden avulla, mutta kyllä esimerkiksi symbolisten laskentaohjelmien tuntemien funktioiden avulla.
Toinen lineaarisesti riippumaton perusratkaisu on tällöin
y = ex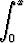
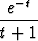 dt
dt
ja homogeeniyhtälön yleinen ratkaisu
y = C1ex + C2ex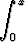
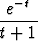 dt.
dt.
Koska integroitavalla funktiolla on nimittäjän nollakohta t = -1, on edellä esitetty ratkaisu pätevä vain alueessa x > -1, jolloin ei jouduta integroimaan nollakohdan yli. Differentiaaliyhtälön ratkaisua voidaan tarkastella myös alueessa x < -1, mutta tällöin on integraalin alaraja otettava tästä alueesta. (Alaraja sinänsä on mielivaltainen, koska etsitään vain jotakin sopivaa funktiota u.) Ratkaisuista vain C1ex jatkuu kohdan x = -1 yli; kaikkien muiden osalta tarkastelualue jakautuu tässä pisteessä kahtia. Tämä näkyy myös siten, että normaalimuodossa olevan yhtälön kerroinfunktioille x = -1 on nimittäjän nollakohta.