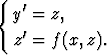
Toisen ja korkeamman kertaluvun yhtälöt voidaan kirjoittaa normaaliryhmän muotoon ja eräissä tapauksissa palauttaa tätä kautta ensimmäiseen kertalukuun.
Tavallisimmat tapaukset ovat seuraavat:
1) Jos toisen kertaluvun yhtälö on muotoa y'' = f(x, y'), on vastaava normaaliryhmä
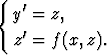
Tässä jälkimmäinen yhtälö on ensimmäistä kertalukua tuntemattomana funktiona z. Tämän ratkaisuna on z(x) = y'(x), jolloin y(x) saadaan yhdellä lisäintegroinnilla.
2) Jos yhtälö on muotoa y'' = f(y, y') — jolloin se on autonominen — on normaaliryhmä
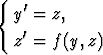 eli
eli 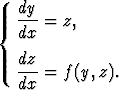
Jos oletetaan, että jollakin tarkastelualueen osavälillä on olemassa ratkaisufunktion käänteisfunktio x = g(y), pätee yhdistetyn funktion z(g(y)) = z(x) = y'(x) derivaatalle ketjusäännön mukaan
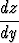 = z'(x)g'(y) =
= z'(x)g'(y) = 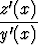 =
= 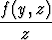 .
.
Täten päädytään ensimmäisen kertaluvun differentiaaliyhtälöön
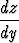 =
= 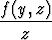 ,
,
joka kuvaa muuttujien y ja z välistä riippuvuutta. Yhtälöön päästään myös jakamalla
normaaliryhmän yhtälöt puolittain ja supistamalla dx pois derivaattasymboleissa 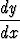 ja
ja
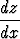 .
.
Tuloksena on siis ensimmäisen kertaluvun yhtälö. Tämän ratkaisu on periaatteessa muotoa z = h(y) tai H(y, z) = 0. Kyseessä on normaaliryhmän ratkaisun y(x), z(x) = y' (x) faasitasoesityksen yhtälö.
Vastaavanlaisia menettelyjä voidaan toisinaan käyttää myös kolmannen ja korkeampien kertalukujen yhtälöiden palauttamisessa ensimmäiseen kertalukuun.