Toisen kertaluvun lineaarinen ja homogeeninen yhtälö

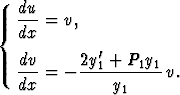
Toisen kertaluvun normaalimuotoinen homogeeniyhtälö on y'' + P₁(x)y' + P₀(x)y = 0, missä kerroinfunktiot P₀(x) ja P₁(x) oletetaan jatkuviksi tarkasteluvälillä.

Yleisen teorian mukaan tämän ratkaisu on muotoa

y = C₁y₁(x) + C₂y₂(x),

missä y₁ (x) ja y₂(x) ovat yhtälön lineaarisesti riippumattomia yksittäisratkaisuja, ts. muodostavat perusjärjestelmän.

Yleistä, so. kaikissa tapauksissa toimivaa menettelyä ratkaisujen y₁(x) ja y₂(x) etsimiseen ei ole. Usein ne pyritään löytämään arvaamalla niiden muoto ja käyttämällä tämän perusteella valittua yritettä.

Jos toinen ratkaisuista tunnetaan, on toisen etsimiseen olemassa seuraava yleinen menettely:

Olkoon y₁ (x) tunnettu ratkaisu. Pyritään etsimään toinen lineaarisesti riippumaton ratkaisu muodossa y₂(x) = u(x)y₁(x), missä u(x) on tuntematon funktio, ts. käytetään yritettä y = u(x)y₁(x). Kun tämä ja sen derivaatat y' = u'y₁ + uy₁', y'' = u'' y₁ + 2u'y₁' + uy₁'' sijoitetaan yhtälöön ja termit ryhmitellään sopivasti, saadaan

u(y₁'' + P₁y₁' + P₀y₁) + u'(2y₁' + P₁y₁) + u''y₁ = 0.

Koska y₁ toteuttaa differentiaaliyhtälön, on ensimmäinen kolmesta termistä = 0. Muut kaksi antavat funktiolle u toisen kertaluvun differentiaaliyhtälön

u'(2y₁' + P₁y₁) + u''y₁ = 0,

jota vastaava normaaliryhmä on

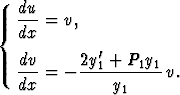
Tässä jälkimmäinen yhtälö on separoituva ja sen ratkaiseminen antaa funktion v (koska P₁ ja y₁ tunnetaan), minkä jälkeen u saadaan yhdellä lisäintegroinnilla.

Funktio u on siis periaatteessa aina ratkaistavissa. Kaikki integroinnit eivät kuitenkaan välttämättä onnistu alkeisfunktioiden avulla.

Funktio u ei ole yksikäsitteinen. Ongelman luonteesta kuitenkin seuraa, että kaikkia mahdollisia funktioita u ei tarvitse määrittää; riittää, että löydetään yksi, joka ei ole vakio (jotta saadaan lineaarisesti riippumattomat y₁ ja y₂).