Epähomogeeninen vakiokertoiminen lineaariyhtälö

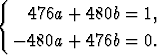
Epähomogeenista vakiokertoimista differentiaaliyhtälöä

y⁽⁴⁾ + 4y''' + 6y'' + 4y' + y = e^-x + sin 5x

vastaava homogeeniyhtälö on

y⁽⁴⁾ + 4y''' + 6y'' + 4y' + y = 0.

Kun tämä ratkaistaan yritteellä y = e^rx päädytään karakteristiseen yhtälöön r⁴ + 4r³ + 6r² + 4r + 1 = 0, jolla on nelinkertainen juuri r = -1. Homogeeniyhtälön yleinen ratkaisu on siten

y = C₁e^-x + C₂xe^-x + C₃x²e^-x + C₄x³e^-x.

Epähomogeeniyhtälön yksittäisratkaisua haettaessa voidaan termit e^-x ja sin 5x käsitellä erikseen. Jos nimittäin y₁ on differentiaaliyhtälön Ly = R₁ ratkaisu ja y₂ on differentiaaliyhtälön Ly = R₂ ratkaisu, ts. Ly₁ = R₁ ja Ly₂ = R₂, niin on myös Ly₁ + Ly₂ = R₁ + R₂ eli L(y₁ + y₂) = R₁ + R₂. Tällöin y₁ + y₂ on yksittäisratkaisu sille yhtälölle, jonka oikeana puolena on summa R₁ + R₂.

Koska e^-x , xe^-x, x²e^-x ja x³e^-x ovat homogeeniyhtälön ratkaisuja, on yhtälön

y⁽⁴⁾ + 4y''' + 6y'' + 4y' + y = e^-x

yksittäisratkaisua etsittävä yritteellä y = Ax⁴e^-x. Tämän sijoittaminen differentiaaliyhtälöön antaa (24A - 1)e^-x = 0, jolloin tulee olla A = 1/24.

Yhtälön

y⁽⁴⁾ + 4y''' + 6y'' + 4y' + y = sin 5x

yksittäisratkaisu voidaan löytää yritteellä y = A sin 5x + B cos 5x. Tämän sijoittaminen yhtälöön antaa (476a + 480b) sin 5x + (-480a + 476b) cos 5x = sin 5x, jolloin tulee olla

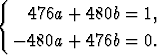
Tällöin a = 119/114244, b = 30/28561.

Kaikkiaan saadaan epähomogeenisen yhtälön yleiseksi ratkaisuksi

y = C₁ e^-x + C₂xe^-x + C₃x²e^-x + C₄x³e^-x + 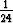x⁴e^-x + 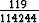sin 5x + 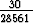cos 5x.