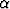 ,
, 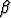 ,
, 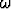 ja n ovat funktion R(x) lausekkeessa olevia
vakioita.
ja n ovat funktion R(x) lausekkeessa olevia
vakioita.
Kertalukua n oleva lineaarinen vakiokertoiminen epähomogeeninen differentiaaliyhtälö on
y(n) + an-1y(n-1) + . . . + a1y' + a0y = R(x),
missä kertoimet ak ovat vakioita. Oikeanpuolen funktio R(x) voi olla millainen tahansa.
Yleisen teorian mukaan epähomogeenisen yhtälön yleinen ratkaisu saadaan summana vastaavan homogeeniyhtälön yleisestä ratkaisusta ja epähomogeeniyhtälön jostakin yksittäisratkaisusta. Viimeksi mainittu voidaan hakea esimerkiksi vakioiden varioinnilla.
Jos kuitenkin kyseessä on vakiokertoiminen yhtälö ja funktio R(x) on sopivaa tyyppiä, voidaan yksittäisratkaisu hakea helpommin yritettä käyttäen.
Millainen yrite on syytä valita vastaamaan tietyntyyppistä funktiota R(x), ilmenee
seuraavasta taulukosta. Symbolit A, B, Ak ovat yritteen parametreja, jotka on määrättävä
siten, että yrite toteuttaa yhtälön; 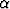 ,
, 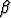 ,
, 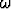 ja n ovat funktion R(x) lausekkeessa olevia
vakioita.
ja n ovat funktion R(x) lausekkeessa olevia
vakioita.
| R(x) | yrite | |
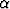 e e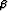 x x | Ae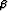 x x | |
Axe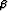 x, x, | jos e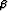 x on homogeeniyhtälön ratkaisu x on homogeeniyhtälön ratkaisu | |
Ax2e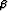 x, x, | jos myös xe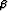 x on homogeeniyhtälön ratkaisu x on homogeeniyhtälön ratkaisu | |
| etc. | ||
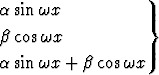 | A sin 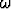 x + B cos x + B cos 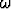 x x | |
Ax sin 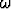 x + Bx cos x + Bx cos 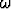 x, x, | jos sin 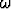 x ja cos x ja cos 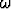 x ovat homog.yht. ratkaisuja x ovat homog.yht. ratkaisuja | |
| etc. | ||
| polynomi astetta n | polynomi astetta n, | |
ts. 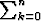 Akxk Akxk | ||
| polynomi astetta n + 1, | jos homog.yht. ratkaisuna on vakio | |
| polynomi astetta n + 2, | jos homog.yht. ratkaisuna on 1. asteen polynomi | |
| etc. | ||
Kutakin funktion R(x) muotoa vastaten on ensimmäisellä rivillä normaalisti
sovellettava yritteen muoto. Jos kuitenkin tämänmuotoinen lauseke sattuu olemaan
homogeeniyhtälön ratkaisu, ei se voi toteuttaa epähomogeeniyhtälöä millään
parametrien valinnalla. Polynomin tapauksessa näin käy, jos karakteristisella yhtälöllä
on juurena r = 0, eksponenttifunktion tapauksessa, jos juurena on r = 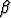 , ja
sini-kosini-tapauksessa, jos juurina ovat r = ±
, ja
sini-kosini-tapauksessa, jos juurina ovat r = ±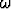 i. Näissä tapauksissa on yritteeseen
lisättävä kertoimeksi x. Jos juuret ovat kaksinkertaisia, otetaan kertoimeksi x2
jne.
i. Näissä tapauksissa on yritteeseen
lisättävä kertoimeksi x. Jos juuret ovat kaksinkertaisia, otetaan kertoimeksi x2
jne.
Taulukkoa voisi jatkaakin, mutta esitetyt tapaukset ovat tärkeimmät. Ne tulevat esiin erilaisissa sovelluksissa, mm. värähtelyprobleemoissa.
Että em. yritteet toimivat, ei ole itsestään selvää. Suorilla laskuilla voidaan kuitenkin osoittaa, että näin on.