Wronskin determinantin differentiaaliyhtälön johtaminen

Wronskin determinantti määritellään homogeenisen lineaariyhtälön ratkaisujen ja niiden derivaattojen muodostamana determinanttina, mutta sille voidaan johtaa yksinkertainen differentiaaliyhtälö, joka näyttää, miten determinantti riippuu vain yhdestä differentiaaliyhtälössä olevasta kerroinfunktiosta. Johto on seuraavassa toteutettuna Maple n keinoin. Lukija miettiköön, millainen tehtävä olisi käsin ratkaistuna (kuten toisen kertaluvun osalta on differentiaaliyhtälöiden kursseissa perinteisesti tehty).

Syötetään aluksi kertaluku ja muodostetaan vastaava normaalimuotoinen homogeeninen differentiaaliyhtälö, jossa kerroinfunktioita merkitään , jne. Differentiaaliyhtälössä korkeimman kertaluvun termi annetaan erikseen, muut voidaan antaa summalausekkeena.

> n:= 3;

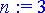
> diffyht:= diff(y(x), x$n)+sum(P[k](x)*diff(y(x), [x$k]), k=0..n-1)=0;

Olkoot , , ... , differentiaaliyhtälön ratkaisuja. Sijoitetaan nämä yhtälöön, jolloin saadaan seuraavat yhtälöt:

> diffyhtsij:= seq(subs(y=y[k], diffyht), k=1..n);

Nämä ovat voimassa kaikilla arvoilla x

Kerätään ratkaisut listaksi ja tätä derivoimalla muodostetaan vastaavat derivaattojen muodostamat listat. Kun nämä kerätään matriisiksi, saadaan Wronskin determinanttia vastaava matriisi. Matriisioperaatioita varten ladataan paketti linalg .

> ratk:= [seq(y[k](x), k=1..n)];

> with(linalg):

> wronskimatr:= matrix([ratk, seq(diff(ratk, x$k), k=1..n-1)]);

Wronskin determinantti on saadun matriisin determinantti. Tämä kehitetään ja sijoitetaan oikeaksi puoleksi yhtälöön, jonka vasempana puolena on Wronskin determinantin symboli (jolle differentiaaliyhtälöä haetaan):

> wronskidet:= w(x)=det(wronskimatr);

Derivoimalla saadaan vastaava Wronskin determinantin derivaattaa koskeva yhtälö:

> wronskidetder:= diff(wronskidet, x);

Wronskin determinantti ja sen derivaatta on saatu lausutuiksi ratkaisujen ja niiden derivaattojen avulla. Toisaalta ratkaisut toteuttavat alkuperäisen differentiaaliyhtälön. Jos näistä yhtälöistä voidaan eliminoida ratkaisufunktiot derivaattoineen, saadaan ehto, joka sitoo Wronskin determinantin, sen derivaatan ja differentiaaliyhtälön kerroinfunktiot. Ennalta ei ole selvää, että tällainen yhteys on olemassa.

Ehtoyhtälöitä on n + 2 kappaletta:

> yhtalot:= {diffyhtsij, wronskidet, wronskidetder};

Eliminoitavia symboleja ovat ratkaisut ja näiden derivaatat; yhteensä n ( n + 1) kappaletta:

> eliminoitavat:= map(op, [seq(diff(ratk, [x$k]), k=0..n)]);

Eliminoitaessa Maple n eliminate -komennolla ei ole mahdollista eliminoida funktioita tai derivaattoja suhteen. Tämä voidaan ohittaa korvaamalla derivaatta- ja funktiomerkinnät väliaikaisilla muuttujilla.

> d2m:= zip((x, y)->x=y, eliminoitavat, [seq(d[k], k=1..4*n)]):

> subs(d2m, [yhtalot, {eliminoitavat[]}]):
eliminate(%[1], %[2]);

Eliminointi onnistuu ja tuloksena eliminate -komento antaa listojen listan, jonka jokainen alkio on mahdollinen ratkaisu. Jokaisen ratkaisun viimeisenä alkiona on eliminoinnin tulos polynomin muodossa. Tarkastelemalla ratkaisuja havaitaan, että on löytynyt 2 erilaista ratkaisua:

ja
.

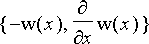Ensimmäinen on yleistapaus ja jälkimmäinen on erikoistapaus, jossa kerroinfunktio supistuu pois. Olemme kiinnostuneita yleisestä ratkaisusta, josta muodostamme Wronskin determinantille ensimmäisen kertaluvun differentiaaliyhtälön merkitsemällä polynomin nollaksi:

> wronskiyht:= diff(w(x), x)+P[2](x)*w(x)=0;

Differentiaaliyhtälö voidaan ratkaista:

> dsolve(wronskiyht, w(x));

Huomaa, että Wronskin determinantti riippuu vain toiseksi korkeinta kertalukua olevan derivaatan kerroinfunktiosta.

Lukija voi muuttaa alussa annettua differentiaaliyhtälön kertalukua ja tutkia, miten Wronskin determinantin differentiaaliyhtälön etsiminen tällöin sujuu.