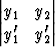 = y1y2' - y2y1'
= y1y2' - y2y1'
Toisen kertaluvun lineaarisen ja homogeenisen differentiaaliyhtälön ratkaisuista y1, y2 ja niiden derivaatoista muodostettu determinantti
W (y1, y2) = 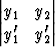 = y1y2' - y2y1'
= y1y2' - y2y1'
on yhtälön Wronskin determinantti (puolalais-ranskalaisen matemaatikon Josef Maria Hoëné Wronskin mukaan; 1778 – 1853).
Korkeampien kertalukujen yhtälöiden Wronskin determinantit muodostetaan samankaltaisella tavalla. Jos kertaluku on n, determinantti on
W (y1, y2, . . . , yn) = 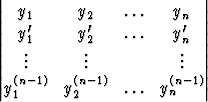 .
.
Tämä voidaan laskea kuten mikä tahansa determinantti kehittämällä jonkin vaaka- tai pystyrivin mukaan, jolloin saadaan lineaariyhdistely n - 1-rivisistä determinanteista. Esimerkiksi j:nnen vaakarivin mukaan kehitettäessä saataisiin
W (y1, y2, . . . , yn) = 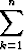 (-1)j+ky
(-1)j+ky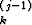 Wjk,
Wjk,
missä Wjk tarkoittaa (n - 1)-rivistä determinanttia, joka saadaan alkuperäisestä poistamalla j:s vaaka- ja k:s pystyrivi. Jokainen determinantti Wjk kehitetään vastaavalla tavalla lineaariyhdistelyksi (n - 2)-rivisiä determinantteja jne., kunnes päädytään kaksirivisiin determinantteihin, jotka lasketaan kuten alussa on osoitettu.
Wronskin determinantin merkitys lineaaristen differentiaaliyhtälöiden teoriassa perustuu siihen, että se totetuttaa differentiaaliyhtälön W ' + Pn-1(x)W = 0, missä Pn-1 on normaalimuodossa olevan differentiaaliyhtälön kertalukua n - 1 olevan derivaatan kerroinfunktio. Tästä voidaan ratkaista Wronskin deteminantti, ilman että ratkaisuja yk on tarpeen tuntea:
W (y1(x), y2(x), . . . , yn(x)) = Ce- Pn-1(x) dx.
Pn-1(x) dx.
Lausekkeesta näkyy, että Wronskin determinantti ei muuta merkkiään, jos normaalimuotoisen differentiaaliyhtälön kerroinfunktiot ovat jatkuvia. Minkä merkkinen determinantti on tai onko se = 0, riippuu vakiosta C eli siitä, mitkä ratkaisut y1 , y2 , . . . , yn ovat kysymyksessä. Tärkein Wronskin determinanttia koskeva lause on seuraava:
Lause. Wronskin determinantti on = 0 (ts. C = 0), jos ja vain jos homogeeniyhtälön ratkaisut y1 , y2, . . . , yn ovat lineaarisesti riippuvia.
Monia muitakin lineaarisen differentiaaliyhtälön ratkaisuja koskevia lauseita voidaan todistaa Wronskin determinanttiin pohjautuen.